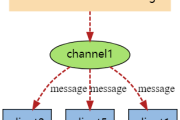
SQL 高级 - GROUP BY 和 PARTITION BY 的含义！

本文将向您介绍GROUP BY和PARTITION BY的含义。

在 SQL 函数中，GROUP BY 和 PARTITION BY 非常相似 - 或者几乎相同。另外，两者都有数学理论基础。本文将围绕集合论和群论中的重要概念“类”来阐明GROUP BY和PARTITION BY的含义。

使用SQL检索异构数据时，一个常见的操作是按照一定的标准组合数据。不仅是在使用SQL的时候，在我们日常生活中对数据进行排序或者分析的时候，我们也经常需要对数据进行组合。

具有分组功能的SQL语句有GROUP BY和PARTITION BY，它们都可以根据特定的列对表进行分组。唯一的区别是GROUP BY 在之后将每个组合并为一行数据。

例如，有一个像下面这样的表，存储了多个团队及其成员的信息。

团队

在此表上使用 GROUP BY 或 PARTITION BY 来检索有关团队的信息。无论采用哪种方式，都可以将原始Teams表拆分为以下子集，然后使用SUM函数合并，或者使用RANK函数计算排名。

SELECT 
  member, 
  team, 
  age,
  RANK() OVER(PARTITION BY team ORDER BY age DESC) rn,
  DENSE_RANK() OVER(PARTITION BY team ORDER BY age DESC) dense_rn,
  ROW_NUMBER() OVER(PARTITION BY team ORDER BY age DESC) row_num
FROM Members
ORDER BY team, rn;

结果：

分割后的子集如下图所示。

一般来说，集合用圆圈表示。不过，为了让“除”（剪切）操作看起来更直观，特意用直线来划分子集。

接下来我们将重点关注分区子集，我们会发现它们具有以下三个属性。

1．全部都是空集合。

2。所有子集的并集等于除法之前的集合。

3．两个子集之间不存在交集。

由于这些子集是由表中存在的“team”列值分割的，因此它不能是空字符串。而且，当所有划分的子集加在一起时，很明显它们是原始集合。也就是说，分区后就没有非专有成员了。

也没有成员同时属于两个小组（=同时属于多个团队）。成员只需属于分区后的某个子集即可。所以我们也可以认为GROUP BY和PARTITION BY都是用来划分团队成员的函数。

在数学中，满足以上三个性质的任意子集称为“类”（划分），将原始集合划分为若干类的操作称为“排序”。这些是群论等领域的术语。划分的类与“分类”中的“类”含义相同，很容易理解。

SQL 中 PARTITION BY 子句的名称来自于类（即分区）的概念。尽管我们可以指定 GROUP BY 子句也使用此名称，因为它按分类执行分组操作，但使用不同的名称以避免歧义。一般来说，集合可以通过不同的方式进行分类。 SQL 也是如此。如果更改 GROUP BY 和 PARTITION BY 列，生成的分组也会相应更改。

在 SQL 中，GROUP BY 的使用非常频繁。由此我们可以知道，我们身边还有很多班级。例如学校的班级、学生的出生地等。没有学生的班级没有任何意义，出生地在两个省份的人不应该存在（可能有出生地不明的人，但这样的人应该属于列为NULL的类别）。

卡片也同样如此。 52张牌按图案可分为4类，按花色可分为红、黑两大类。同一类的元素满足与朋友相同的标准 - 至少与另一类的元素一样接近（从数学上讲，这种关系称为“对等关系”）。用一个不太恰当的词来说，就是“物以类聚，物以类聚”。

在群论中，划分类根据不同的分类方法有不同的名称。群论中有很多非常有趣的类，比如“留数类”。顾名思义，它指的是类除以整数的余数（一般情况下，类不一定是数字的集合，但现在我们只考虑数字的情况）。

例如，将自然数集合N对3进行余数排序后，我们将得到以下3类。

残留类别 0：M1 = {0, 3, 6, 9, …}

残留类别 1：M2 = {1, 4, 7, 10, …}

残留类别 2：M2 = { 2, 5, 8, 11, ...}

从第二类性质，我们知道这三类涵盖了所有自然数。这种情况可以用下面的公式来描述。

M1 + M2 + M3 = N

我们将这 3 个类别称为“ 模 3 剩余类别 ”。 Modul指除数，英文为Modulo。与类相比，模块的概念有些抽象且难以理解。

该模块也是用SQL实现的，是一个模MOD函数。尽管标准 SQL 中没有定义，但它在大多数数据库中实现（SQL Server 中使用 % 运算符）。在 SQL 中，它的常用用法如下。

--对从1到10的整数以3为模求剩余类
SELECT 
  MOD(num, 3) AS modulo,
  num
FROM Natural
ORDER BY modulo, num;

结果：

残基类还具有许多有趣的特性，并且可以具有广泛的应用。例如，残差类搜索会将自然数集合划分为若干个大小相等的类，因此当需要从大量数据中采样一定比例时非常方便。例如，使用以下查询语句将数据随机收缩到原始大小的五分之一（如果表没有连续编号的列，只需使用 ROW_NUMBER 函数对其进行重新编号）。

--从原来的表中抽出（大约）五分之一行的数据
SELECT ＊
FROM SomeTbl
WHERE MOD(seq, 5) = 0;

--表中没有连续编号的列时，使用ROW_NUMBER函数就可以了
SELECT ＊
FROM (SELECT col,
             ROW_NUMBER() OVER(ORDER BY col) AS seq
     FROM SomeTbl)
WHERE MOD(seq, 5) = 0;

当然，在现实中，表中数据的行数可能不完全是5的倍数，因此其余类的大小也不一定相同。但是，上面的查询语句绝对满足“将数据随机等分”的随机采样要求。

这篇文章是不是让你对的实现过程GROUP BY和PARTITION BY以及它们的数学基础有了更深入的了解呢？总的来说，SQL和关系数据库引入了大量集合论和群论的结果。

你可能会觉得这些内容有点抽象。嗯，它们确实很抽象，但正是因为它们的抽象性，它们才被广泛使用。数学理论不是脱离现实的游戏。事实上，它隐藏了许多我们可以在日常工作中使用的技能。但如果你只是等待，就很难找到它们了。数据工程师只有通过自己的努力搭建起理论与实践之间的桥梁，才能提高数学应用能力。