通过比较经典的例子讲解一些常用的算法思想。常用的算法思想包括:枚举、递归、分而治之、贪心、启发式、动态迭代和模拟等。本节我们学习枚举算法。
1。枚举思想
枚举算法也称为穷举算法。该算法使用所有方法来解决问题,并通过推理来考虑事件。所有的可能性,最终都有一个结论。
在Python中,我们一般通过while语句或者if语句来实现枚举算法。具体思路如下:
首先分析问题的对象、范围和判断条件,然后将所有符合条件的解决方案一一列出。
枚举算法的流程图如下:
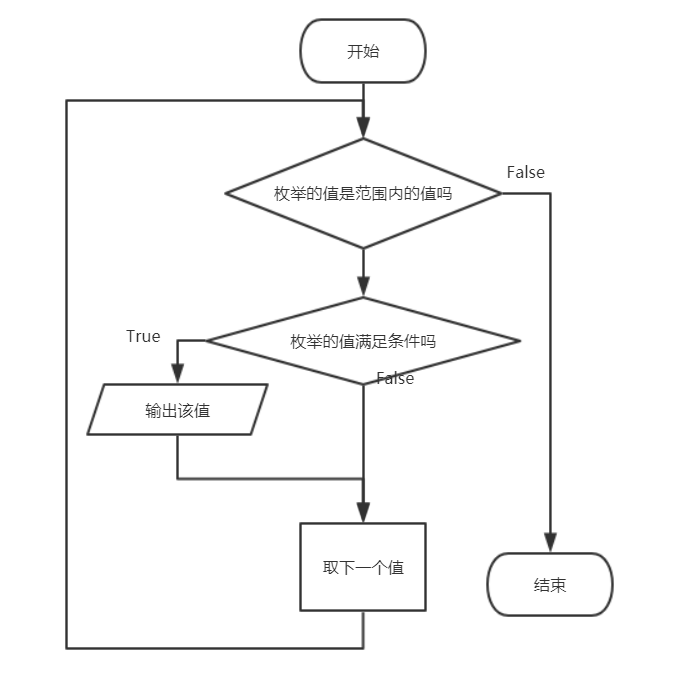
首先判断值是否在范围内,然后判断是否满足条件,最后输出或移除一个值,直至结束。让我们通过例子来学习这个算法思维。 ?例如:153是水仙花数,因为153=1^3+5^3+3^3。
那么这道题的取值范围是100-999,条件是每个数字的骰子之和等于自己,那么我们看代码:
| 123456789 | 计数= 0对于 我 在 100,1000): 计数+ = a = ♺int ) b = int(i/ 10 | 123456789 | ) c = int(( i )) 如果(c,♹)=我: print( '水仙花数量:',i)print ( ❙'计数次数:') 结果为: | 12345 | 水仙花数量: 153 水仙花数量: 370 水仙花数量: 371 水仙花数量: 407 Enumer 的数量: 计算值范围为 100-999 ,然后通过判断是否输出的value满足条件,最后输出枚举数。这是一个比较简单的枚举问题。 3。 100元买100只鸡 母鸡每只5元,母鸡每只3元,三只小鸡1元。 100元买100只鸡。问公鸡、母鸡和小鸡各有多少只? 我们先来分析一下: 如果只买公鸡100元,可以买20只公鸡,母鸡最多只能买33只,小鸡可以买300只。 我们可以通过枚举的思想来解决这个问题,通过两层循环和一层判断就可以完成。范围 (20): 对于然后在 范围):( 鸡= - 母*♂ == 100: 打印(370' + 鸡 %d + 鸡 %d d = 100只鸡。'%(公鸡,母鸡,母鸡)) |
输出结果为: 公鸡仅 + 母鸡25 + 小鸡 75 N75 = 鸡。公鸡4仅 +母鸡100鸡。公鸡8仅限 +母鸡100鸡。仅母鸡12+母鸡4仅++=100鸡。在这道题,我们首先分析鸡存在的可能性,由于鸡的价格是五元,所以我们最多可以买20只,鸡的价格是3元,所以我们最多可以买33只。那么我们先用一层循环覆盖狗的数量,从1到20,然后使用一层循环来确定狗的数量。这时一百减去此时母鸡的数量和公鸡的数量。数字之和就是鸡的数量,然后用if语句判断当前三类鸡的总和是否等于一百,如果满足条件则输出。4。总结 关于枚举算法,它的优点是,枚举方法一般是现实生活问题的“直译”,因此更加直观、容易理解;枚举法基于对大量状态的检查,也基于对所有状态的穷举枚举,算法的正确性更容易证明。当然,他们的缺陷也很明显。使用枚举法解决问题的最大缺点是计算量比较大,解决问题的效率不高。如果枚举方法的范围太大(一般限制不超过200万次),从时间上来说是不可持续的。不过枚举算法思想简单,程序编写和调试实用,比赛时很容易思考。在比赛中,时间是有限的,我们比赛的最终目的是找到问题的解决方案。因此,如果问题的规模不是很大,如果能够在规定的时间和空间限制内找到解,我们最好使用枚举法,而不必过多担心是否有更快的算法给出。这使您有更多的时间来解决其他难题。 |
|
版权声明
本文仅代表作者观点,不代表Code前端网立场。
本文系作者Code前端网发表,如需转载,请注明页面地址。
![]()
 code前端网
code前端网



