什么是回溯算法？框架例程详解VS leetcode案例分析

terry 2年前 (2023-09-27) 阅读数 80 #数据结构与算法

刷leetcode的时候，经常会遇到回溯算法的问题。回溯算法是五种基本算法之一，大多数大厂也喜欢询问。下面我们一起来学习一下回溯算法例程。

1。什么是回溯算法

回溯算法是通过探索所有可能的候选解来找到所有解的算法。

它采用试错的思想，尝试一步步解决一个问题。在逐步解决问题的过程中，当它试图发现现有的逐步答案无法得到高效正确的答案时，它会中断上一步甚至前几步的计算，然后使用其他可能的解决方案。步骤答案再次尝试寻找问题的答案。回溯方法通常采用最简单的递归方法来实现。反复重复上述步骤后，可能会出现两种情况：

找到可能的正确答案；
尝试所有可能的分步方法后，声明问题没有答案。

举一个生活中类似的例子，例如，牧羊人在十字路口丢了羊。他沿着不同的十字路口寻找羊，并试图在十字路口找到羊。如果找不到羊，就继续往回走，在岔路口寻找另一条路，直到找到羊。

下图是找羊的路线图：

牧羊人向A方向看，然后向C方向走，没有找到就回到支路，向D方向走...直到他找到了羊。这是原路返回。

2。算法查询进入回溯算法

给出一个不重复数字的数字数组，返回其所有可能的排列。您可以按任意顺序返回答案。？酒吧。比如要对3个数字[1,2,3]进行排序，想先对1进行排序，那么第二个数字就只能是2或3。如果第二个数字是2，那么第三个数字就只能是3 ...

我们可以根据羊的路线图来找到羊，画出一个完整排列的树图，如下：

其实我们是从根节点开始遍历这棵树，记录沿途的数字路径，走到叶子节点的时候就可以得到一个排列。遍历完所有叶子节点后，就可以得到整个排列。

我们怎样才能更清楚地理解这棵树呢？

为了方便理解，我们可以将nums的数字k看成k选择。例如，对于 [1,2,3]，每个数字有 3 个选择： 1, 2, 3 。
每次你做出选择，空间树就会展开。
选择后，如果所选路径重复，请将其裁剪。

上图中的树可以看作是遍历所有元素，扩展空间树，然后进行剪枝。如下图

好啦，既然我们知道了这棵树是从哪里来的，那么我们来看看如何遍历来找到整个排列吧？每次你走下树上的树枝，就像做出一个决定。我们可以将已经路径和可用选择视为树节点的两个属性。

如果在根节点，可选择的有1、2、3，遍历的路径为空，如下图

到达叶子节点时，遍历的路径长度相等到元素组的数量。此时，经过了路径，这是满足条件的解。

2.2 代码实现

如何编写代码？以前学习树遍历的时候，我们通常会使用递归。这道题也用到了递归。

什么是递归项？一条可选的路径和一条已经走过的路径就可以了。
递归函数体呢？ for 循环枚举当前数组的元素，需要 if 计算来跳过修剪
递归退出怎么样？也就是说，我们去叶子节点。叶子节点是当构造的路径path的数组长度等于nums

的长度实现代码如下：Why do we need: What about回溯？或者说为什么要使用回溯算法？

因为我们不只是要找到一个排列，而是需要找到所有满足条件的排列
当递归调用结束时，当前的递归分支结束，我们还要去其他分支继续搜索
因此，必须取消当前选择，返回到选择前的状态，然后选择下一个选项，即进入下一个分支。？关于问题的问题，依据也是穷举。我们通常通过穷举找到模式，然后绘制回溯决策树。例如，在上面的示例中， 排列在 中。
决策树的节点一般有两个属性，即已经采取的路径和已经可用的选择。总结决策回溯树时需要小心。
3.2。使用回溯算法框架
确定回溯问题实际上就是解决决策树的遍历过程。必须考虑这三个问题：
- 采取的路径：做出选择，走过的路
- 可选列表：当前可以做出的选择
- 最终条件：通常走到决策树的叶子节点，无法再进行其他条件选择
回溯算法的伪代码框架如下：
```
//所有路径集合
List<> allPath  = []
void backTrace (可选列表，已走路径)：
     if(满足结束条件){
        allPath.add(已走路径);
        return;
     }
     for(选择：可选列表){
        做选择
        backTrace（当前可选列表，已走路径）;
        撤销选择
     }
```
4. Leetcode案例研究
标题：
给你一个没有重复元素的整数矩阵候选者和目标整数候选者的组合可以得出总和数字目标，并以列表形式返回。您可以按任意顺序返回这些组合。
候选者中的相同号码可以重复选择，不受限制。如果至少有一个数字选择不同，则两种组合是不同的。？ = 7：
```
7 = 2 + 2 + 3
7 = 7
```
再看一下例2的数据：
```
8 = 2+ 2 + 2 +2
8 = 2 + 3 + 3
8 = 3 + 5
```
其实规律还是比较清晰的。我们只需要从候选数组中一一提取目标即可。如果元素可以减少到0，那么它就是一个解决方案。
下一步是画树。我们可以将目标视为树的根节点，然后分支分别代表射线候选候选的中间元素。然后子节点target减去数组元素之间的差值，如下：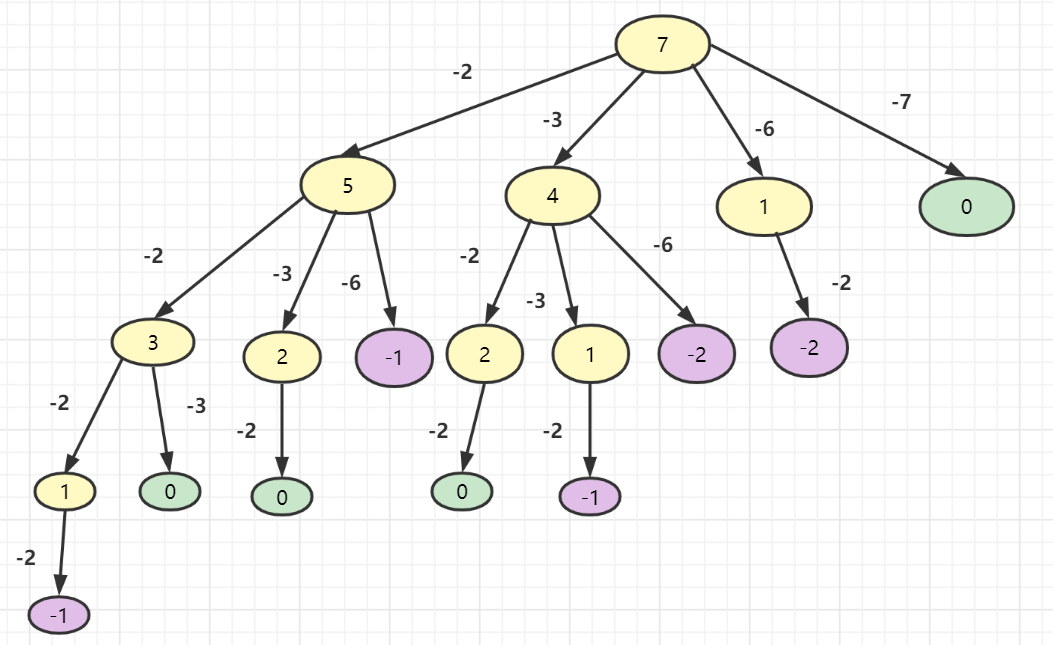
然后我们就可以使用回溯算法框架了。如何表达所采取的路径、可选列表和退出条件？看下图：
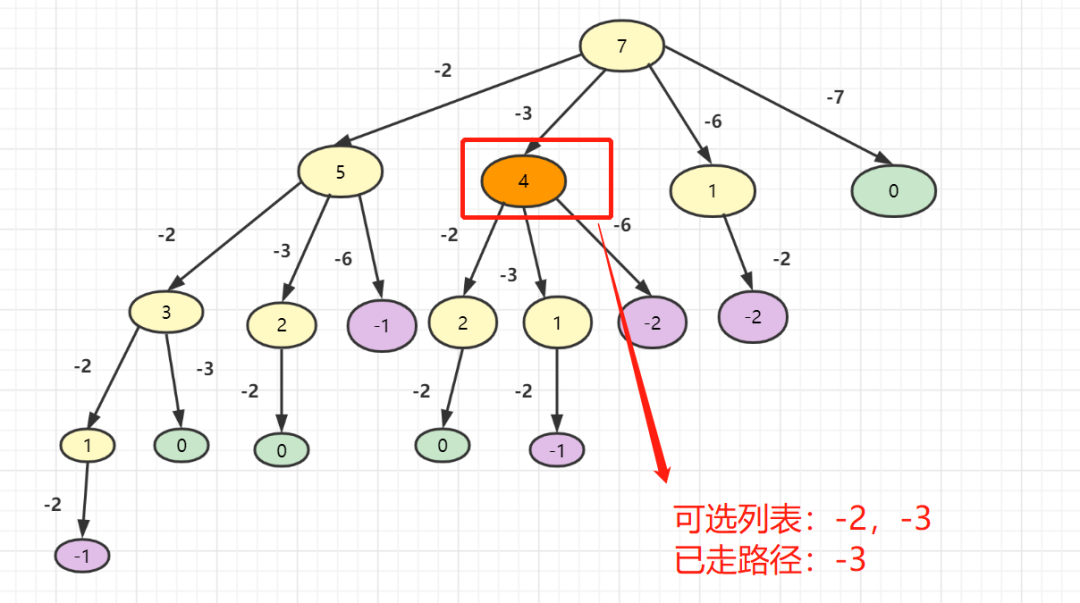
如果到达橙色节点 4，可选列表是减 2，或减 3，因为减去 6 是负数。你怎么知道这是一个可选列表？只要当前目标减去要选择的分支的值大于0，就可以用作可选列表。
所采取的路径是分支-3。
最后的条件呢？当你到达为负数或0的节点时，就意味着是时候退出了，你无法再做出决定。？