高斯滤波器原理及其代码实现过程

高斯滤波器是一种线性滤波器，可以有效抑制噪声，平滑图像。其工作原理与平均滤波器类似，将滤波器窗口内像素的平均值作为输出。该窗口模板的系数与中值滤波器的系数不同。中值滤波器的模板系数全部相同，均为1；而高斯滤波器的模板系数随着距模板中心距离的增加而减小。因此，高斯滤波器对图像的模糊程度小于中值滤波器。

什么是高斯滤波器

顾名思义就是高斯滤波器，它和高斯分布（正态分布）有一些联系。二维高斯函数如下： 其中(x,y) (x,y)是点坐标，在图像处理中可以认为是整数； σ 是标准差。对高斯函数进行采样可以得到高斯滤波器模板，得到的高斯函数值作为模板系数。例如：生成3×33×3高斯滤波器模板，则以模板的中心位置作为采样坐标原点。模板在每个位置的坐标如下（x轴水平向右，y轴垂直向下）这就是每个位置的坐标输入到高斯函数中，得到的值是模板的系数。 如果窗口模板的大小为(2k+1)×(2k+1)，则模板各元素值的计算公式如下： 这样计算出的模板有两种形式：小数和整数。

• 十进制形式的模板是直接计算出来的值，无需处理；
• 整型模板需要进行归一化，将模板左上角的值归一化为1，如下详细介绍。使用整数模板时，必须在模板前面添加系数。系数为，即模板系数之和的倒数。

高斯模板生成知道模板生成原理的话实现起来并不难voidgenerateGaussianTemplate(double window[][11], int ksize, double sigma){{❀ static const double pi = 3.1415926; int center = ksise / 2; // 模板中心，坐标为 double x2, y2; (int i = 0; i { {2; ); double g = exp(-(x2 + y2) / (2 * sigma * sigma)); g /= 2 * pi * sigma; window[i][j ] = g ; } } 双 k = 1 / 窗口[0][0]; // 将左上角系数归一化为 1 for (int i = 0; i { for (int j = 0; j window[i][j] *= k; } }} 假设一个二维数组来存储这里生成的系数（这是最大生成的系数模板大小不超过11​​）；第二个参数是模板的大小（不超过11​​）；第三个参数比较重要的是高斯分布的标准差。 生成过程首先根据模板尺寸找到模板ksize/2的中心位置。然后根据高斯分布函数计算模板中每个系数的值来进行遍历。 需要注意的是，在最后的归一化过程中，将模板左上角的系数的逆作为归一化系数（将左上角的系数值归一化为1），并且每个模板中的系数是乘以该值（左上方系数的倒数）并对所得值进行舍入以获得整数高斯滤波器模式。下面的截图生成了一个大小为3×3的模板，σ=×3，σ=将上面的求解结果四舍五入后，得到如下模板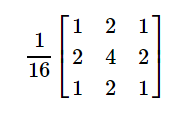： 这个模板比较熟悉，是基于高斯函数 σ= 生成的模板。 至于生成十进制形式，就比较简单了。去掉归一化过程，在求解过程之后，将模板的每个系数除以所有系数的总和。具体代码如下： voidgenerateGaussianTemplate(double window[][11], int ksize, double sigma){ static const /double pi = 2 int /ksi center = 3.1415926; ; // 模板的中心，即坐标 double x2, y2; double sum = 0; for (int i = 0; i { x2 = pow(i - 中心, 2); 对于 (int j = 0; j { y2 = pow2); double g = exp(-(x2 + y2) / (2 * sigma * sigma)); g /= 2 * pi * sigma; sum += g; ][j ] = g ; } } //double k = 1 / window[0][0]; // 标准化左上角系数 1 for (int i = 0; i { for (int j = 0; j window[i][j] /= sum; } }} 十进制模板 3×3，σ=. σσ值的意义和选择通过上述实现过程，我们不难发现，生成高斯滤波器模板最重要的参数是高斯分布的标准差σσ。标准差表示数据的分散程度。当σσ较小时，生成的模板中心系数较​​大，周围系数较小，因此对图像的平滑效果不是很明显；相反，当σ较大时，生成的模板 模板的系数差别不大，与平均模板更加相似，对图像的平滑效果更加明显。 查看具有以下维度的高斯分布的概率分布密度图： 横轴表示 x 的可能值，纵轴表示概率分布 F(x) 的密度。那么这样一条曲线和x轴的周长就不难理解了。生成的图的面积为 1。 σσ（标准差）决定了图的宽度。可以得出，σ越大，图形越宽，峰值越小，图形越平坦； σ越低，图形越窄、越集中，中间部分越尖锐，图形变化越剧烈。其实很容易理解。如果标准差 sigma 较大，则意味着密度分布必须更加分散。由于面积为1，峰分数减少，宽度更宽（分布更分散）；同样，如果 σ 大于小，则意味着密度分布更集中，因此峰越尖锐，宽度越窄！ 可以得出以下结论：σσ越大，分布越分散，各部分比重差异较小，因此生成模板的元素值存在差异​​不大，与一般模板相似； σσ越小，分布越集中，中间部分所占比重远高于其他部分。正如高斯模板中所体现的那样，中心元素的值远大于其他元素的值，因此自然相当于中点运算。基于OpenCV的实现这对于生成高斯模板很有好处。其简单的应用与其他房间过滤器没有什么不同。具体代码如下： void GaussianFilter(const Mat &src, Mat &dst, int ksize, double sigma){ CV_Assert(()3 || () == 3); // 只处理单通道或三通道图像 const static double pi = 3.1415926; // 根据窗口大小使用 sigma 生成高斯滤波器模板 // 用于存储为 double 数组生成的高斯模板矩阵 double * *templateMatrix = new double*[ksize]; for (int i = 0; i templateMatrix[ksize] = new double*[ksize] ]; int 原点 = ksize / 2; // 以模板中心为原点 x2 = pow(i – origin, 2); for (int j = 0; j { y2 = pow(j – origin, 2) ) ; //高斯函数之前不需要计算常数，在归一化过程中被消除 double g = exp(-(x2 + y2) / (2 * sigma * sigma) ); sum += g; templateMatrix[i][j] = g; } } for (int i = 0; i { templateMatrix[i][j] /= sum; cout