红黑树数据结构看似复杂，但是结合2-3-4树

terry 2年前 (2023-09-27) 阅读数 67 #数据结构与算法

就不难理解了。红黑树是一个比较复杂的数据结构。相信很多人只知道它的名字，却不知道它的含义。因为理解它的原理需要花费一些努力。我写这篇文章的原因是为了更好地理解Java中TreeMap的源代码。

写之前，我在网上搜索了文章。说实话，读完之后我有点困惑。大多数都会立即给你它的五个主要属性，然后是简单的插入、删除和旋转操作。就是这样，很难理解。

本文将结合2-3-4树，逐步将红色的起源和❀和❀介绍树a❀ 。我相信读完本文后，您一定会喜欢的。有了更清晰的认识。此外，需要注意的是，这里描述的是普通红黑树，而不是它的变体左切红黑树（LLRB）。

红黑树的介绍

二叉搜索树

红黑树的起源是从二分搜索树开始的。二叉搜索树是一棵二叉树。每个节点的值都大于其左子树中的所有节点并小于其右子树中的所有节点。它结合了链表插入的灵活性和有序数组搜索（二分搜索）的效率。

对于使用二叉搜索树的算法，其运行时间取决于树的形状，而树的形状取决于节点插入的顺序。如上图所示，最好的情况，N节点的树是完全平衡的，每个空链接到根节点 N的距离;最坏的情况是，搜索路径上可能有N个节点退化为链表。

所以，为了保证我们动态构建二叉搜索树时，运行时间始终处于对数级别，我们希望降低它的平衡❀，，树，这样就应该有尽可能多的~lgN，这样每次查找都能保证并且~lgN二分查找，这样一棵树就变成了称为平衡二叉搜索树。

AVL树

第一个自平衡二叉搜索树是AVL树自平衡二叉搜索树是AVL树 ❀❀不超过1。放置或删除节点并打破平衡后，它会通过一次或多次树旋转重新平衡。

AVL树是严格平衡，适合精细密集型应用，因为在频繁插入或删除顶点的场景中，会花费树旋转的成本

和太高。
并且红黑树 是一个 妥协解决方案。它不追求完美平衡，而只追求部分平衡，所以减少了调整时树木旋转的次数。
2-3-4树
说到红黑树就不得不提2-3-4树因为其中一棵可以说红黑树特殊实现
，了解一些，对于理解红黑树很有帮助。
保持平衡无非就是降低树的高度。如果二叉搜索树被广义化，允许一个节点存储多个值，它就变成了多叉树。也可以认为是身高的降低。
准确地说，标准二叉搜索树中的节点称为2-node （具有两个子节点的值）。现在引入3-节点（两个值和三个子节点）和4-节点（三个值和四个子节点），这样就得到了2- 3-4 树
（也称为冷杉2-4 树）。
2-3-4树是一棵4阶B树，所有数据按排序顺序存储，所有叶子节点的深度相同。对于大多数编程语言来说，直接实现2-3-4树是很困难的，而实现红黑树则相对容易和简单，这也是红黑树被广泛使用的部分原因。
红黑树是二叉树，所有节点都是2个节点，所以为了能够表示4个数，引入了节点颜色属性：
黑色，代表普通节点
红色
多值节点

如上图所示，如果红色平放的红黑树的节点

及其父节点将与左侧的2-3-4树相同。
红黑树
现在我们看一下红黑树的属性：
每个节点都是红色或黑色
根节点是黑色（末端会变黑）

全部叶节点是黑色的。这里的叶子节点指的是空节点，常用的NIL子顶点都是黑色的（红色表示可以与父节点合并）节点，这是子节点的乐趣）

从给定节点到其任何后代到NIL节点

的每条路径都包含❀相同数量的黑色顶点（在转换后的2-4树，所有叶子节点都在底层）

这个属性没必要记住，即使你❝记住了，你也一定会忘记。应该结合2-3-4树来理解记忆，另外，将和旋转成红黑树，相当于分裂成 2-3-4树合并，2-3-4树节点的分裂和合并很容易理解。对比分析和理解红黑树的运作绝对会让你眼前一亮。

树旋转

在分析插入和删除之前，我们先来了解一下树旋转是什么。树旋转是对二叉树中子树

进行调整的操作。它经常被用来调整树的局部平衡。它包含两种方法，左旋转和右旋转。
实际上，旋转操作易于理解：left旋转
是两个顶点中较小的节点，与右旋正好相反，如上图所示：
右旋，即以中最小的一个作为根节点，然后匹配L和P的子树
向左旋转，即使用较大的 P作为根节点，然后从P调整红黑树的
而L旋转实际上是保证与结构相同的2-3-4树一一对应，同时保证红黑树的有序性和平衡性。
插入
接下来我们结合2-4树来分析节点的插入。首先，2-4树的插入逻辑如下：
如果是2节点，直接插入变成3节点
如果是3节点，直接插入变成4节点如果是4节点，先拆分，变成2节点，，然后放入
2-4。树设置所有 叶子节点 、红黑树 设置所有节点

是节点要插入的被认为能够插入到多值节点。

假设引入的节点N，P是❙的父节点❙G是的祖父节点N ，U是N的僧节点，那么红树有以下插入情况：

N是根节点，即父节点红色树的第一个节点
的节点（P）是黑色
P是红色（不是根节点），以及它的兄弟节点

也是U red

P 是 Red，并且 U 是黑色1

这三种情况都比较简单，所以放在一起解释。都是，不涉及旋转，只涉及颜色翻转，换句话说只是合并❀节点，没有分裂。

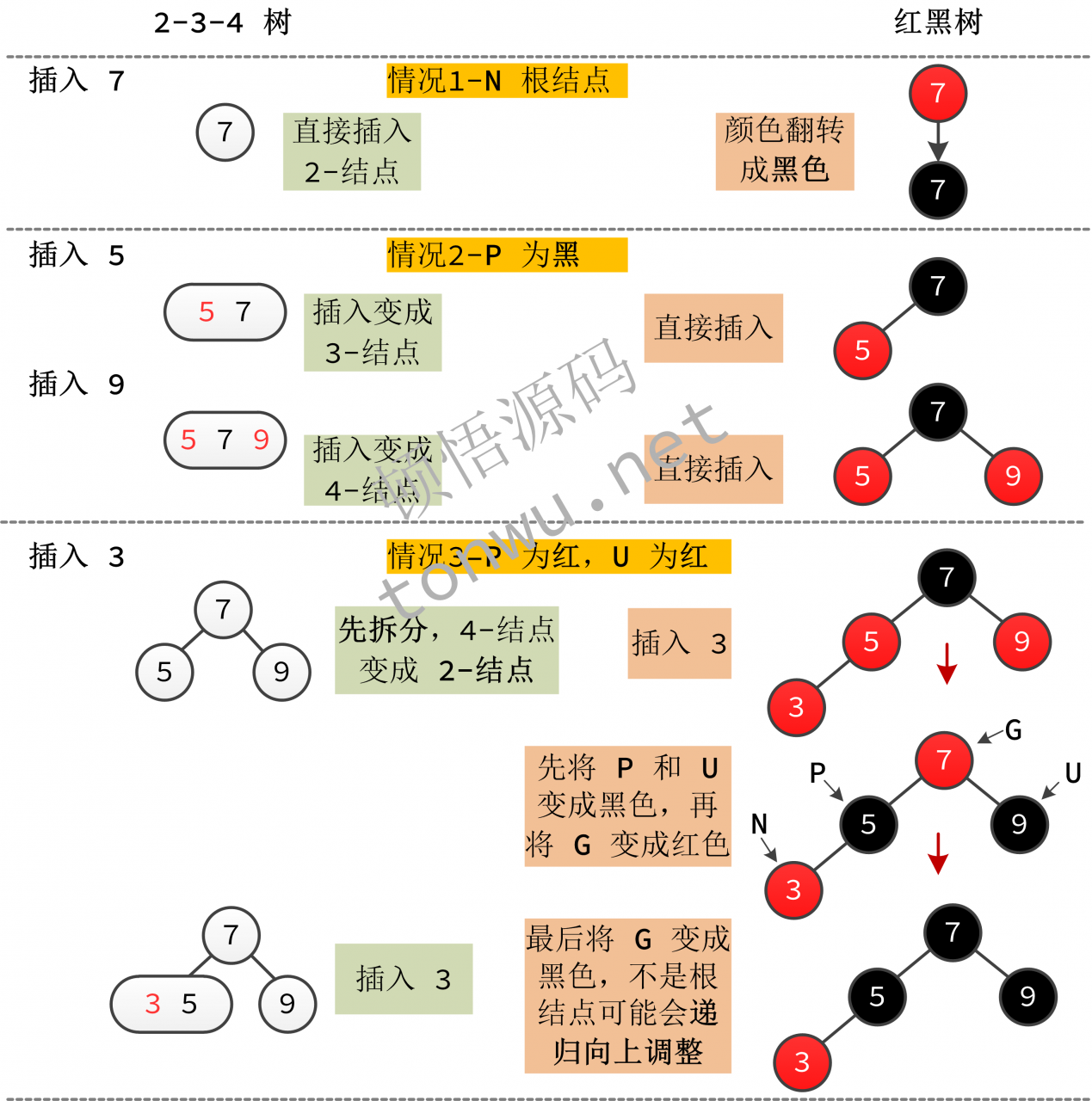
情况1和2不会影响红黑树的属性，也不会破坏平衡。可以直接插入：

对于2-4树，空树插入 2- Node->3-Node->4-Node 转换过程黑树为默认与根节点黑色2-节点

情况3建立，P是

U也是 红色，两棵树的插入情况如下：

在2-4树中，这是一个-节点，首先进入2-节点被分裂，然后为红黑树引入
，相当于它们被分裂并立即变色：和U变成黑色，G变为红色，如果❀是的根节点，则立即变黑，否则向上递归检查是否有 上不平衡以[7,5,9,3]❙为例。两个树构建过程如下：
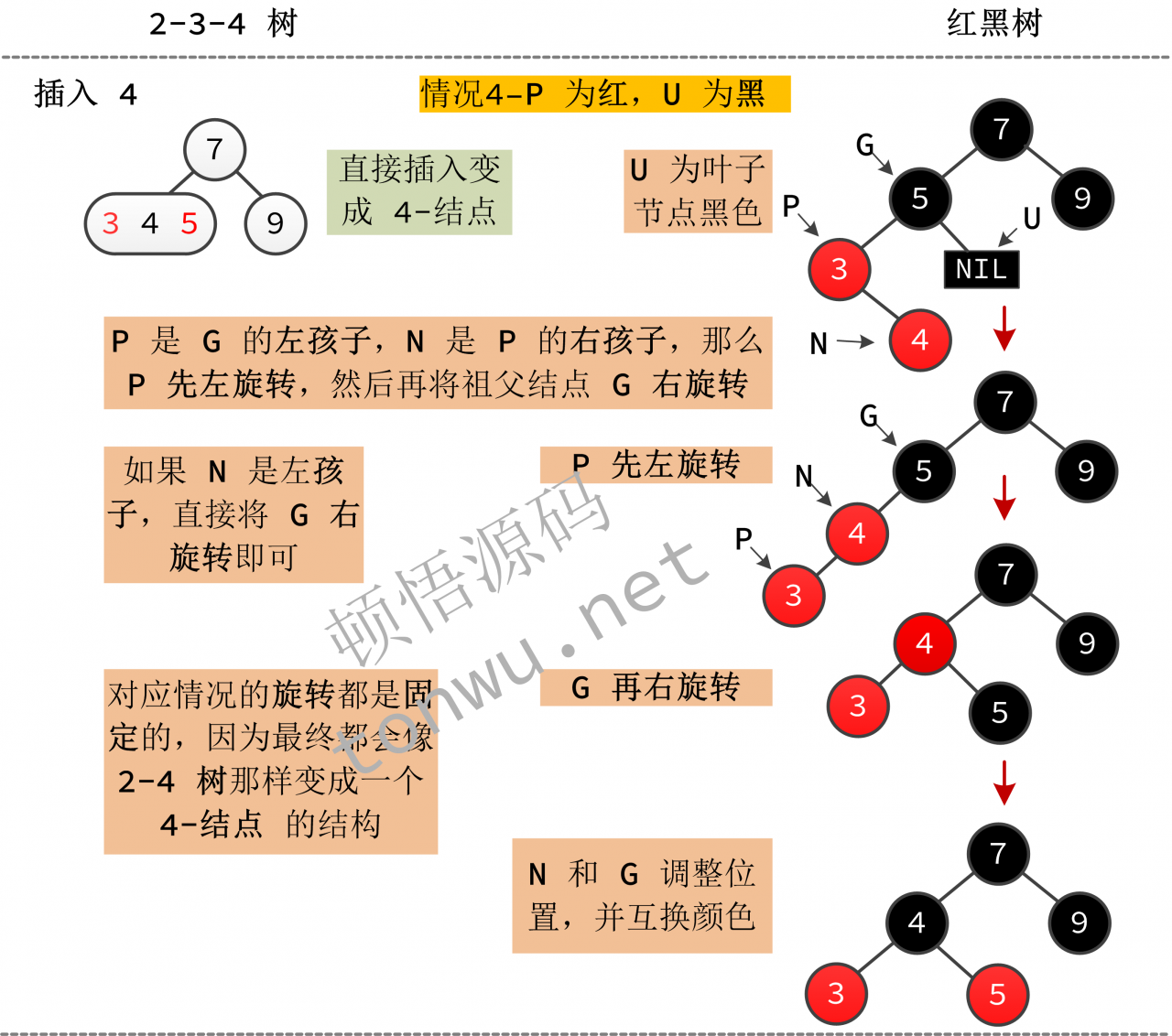
Case 4
Case 4，P为❀和U 是黑色的。此时，在2-4树中，该节点是3-节点，直接插入到4-节点；至于红黑树，为了与2-4树结构保持一致，它会根据不同的情况进行轮换。有四种可能性：
P 是 G 的 左孩子如果 P 是
的
，然后旋转祖父节点G右可以
P是左孩子G如果N 没错 P 孩子，然后 P⸀
G 右 G 右的子，如果N 是右子，则旋转G 左 即
P 是 G 的 真正的孩子 ，如果如果P是左孩子，那么P先直转，然后爷爷左转[ 7 , 5 , 9, 3 , 4]以输入序列为例，即根据上图，设置4，则表示P为左边，❀N 为右边，树的旋转过程：
其他情况左右可以互换。你可以试着分析一下自己。这里给出了红黑树和2-3-4树。她的动态构建过程，输入顺序为[7,5,9,3,4,8,10,11,12,13,14,♝,共 2 -3-4 构建树：
红黑树构建过程中，有根节点调整不要：删除
的按钮二叉搜索树无非就是有两个子节点、有一个子节点和三种，其中有两个子节点 。 M节点的删除逻辑为：
先看M节点的Max est 的左子树 右子树的 X
然后将X节点的值复制到
后面点击，最终删除问题简化为：最多有1个节点删除子，所有删除操作都是在叶子按钮上完成，但是删除的节点不是我一开始想删除的节点，而是节点的值最后被删除了，变化与问题的简化相比，树结构的变化并不重要。
在分析红黑树的删除之前，我们先简单看一下2-3-4树的删除。？合并节点主要有3种不同的情况：
如果元素K是一个内部节点并且至少是一个键，如果它在'至少上是。元素K
位于叶子节点
中，只需将其从节点中删除即可。如果元素K是一个内部节点，并且有左子节点和右子节点，则：
2.1 如果左子节点至少有2个键，则找到一个最大值来替换K，然后删除这个最大值
2.2 如果右孩子至少有2个键，则找到一个替换K
然后删除
，然后删除最小值

2.3 如果两个子节点都只有 1 个键，则下沉 K 并将其与其子节点合并以形成至少一个。具有2个key的节点最终被删除，元素K不是内部节点，并且它所在的节点只有1个key，那么根据以下情况，最终变成情况1 或转换后的情况 2:
3.1 如果其兄弟节点至少有 2 个 key，则选择其中一个并将其推送到父节点，然后将旧父 Shen 加载到 K ❝❝ 3.2 如果其同级节点也只有 1 个 key，则将父节点下沉，与其子节点合并，然后删除 K, 所以 ❀, ❀ 父节点必须至少有 2 个键 。如果没有，则在父节点上按照情况3递归处理

以上情况。有一个条件，即遍历查找要删除的节点时，必须确保节点经过的至少有2个钥匙。如果没有，则需要合并节点。这一点很难理解。如果插入，那么遍历过程中遇到的4个节点就变成了❀。相比之下，在中，如果删除，则需要保证遍历的顶点至少有2个键，相当于合并。

下图展示了上面提到的每一种可能的删除情况：

简单来说，理解2-3-4树删除的要点就是：删除了❝多有价值的节点，请立即删除它们

否则从兄弟节点获取额外的节点来填补空缺父节点单击以获取节点来填补空缺。如果父节点没有多余的节点，则在父节点上重复问题进行处理。

红黑树的删除

红黑树的删除也和二叉搜索树类似，但是必须考虑平衡，也就是节点颜色问题，稍微麻烦一点。

首先，声明一些。接下来，红色和黑色树叶按钮和二元搜索树叶按钮是相同的。如果要强调红黑，当树节点为空叶子节点时，特声明NIL，绘图时用黑框表示。

假设要删除的节点为M。如果有非叶子节点，则称为C。那么有两种比较简单的删除情况：

M是红色节点，那么它的一定是叶子节点，直接删除就可以了，因为如果它有黑色的非叶子节点，会伤害它属性5，经过M向左或向右的路径有几个黑色顶点。
M 为黑色，C 为红色。将C替换为M 并使其变黑，或者交换C❀C❀和的值，并且删除 C （这是第一个简单条件）。

注：M 仅有一个非叶左或右子节点，对应于树情况1。

这两种情况，本质都是去掉一个红结，不影响整体平衡。以[7, 5, 9, 3, 4]构造的红黑树为例，演示一下上面比较简单的情况：

比较复杂的删除是❀ 2 肯定是NIL 节点，如果不是这样，就会违反性质5。

删除黑色节点会打破平衡。你必须找到一个节点来填补的空缺。假设要删除的节点为M。删除后，其位置发生变化。有 NIL 节点。为了描述方便，将该节点记为N，P表示N of of。 代表N兄弟节点，S如果有左右子节点，则分别使用SL。 SR表示，那么删除有以下几种情况：

情况1 - N为根节点

删除后变成 N❝ N❝r ,即删除前只有一个节点M，可以立即删除。

情况2 - P black S red

S是红色，那么它必须有两个子节点，都是黑色的，并且P也必须是黑色。此时，将P和S的颜色互换，然后将P

向左旋转，根据：N 父节点变为红色，姐妹节点变为SL。此时可以按照情况4、5、6继续处理。

情况 3 - P Black s Black

p 是黑色，s 也是黑色，s 也没有非空孩子。此时，S立即变为红色，则通过S的路径将作为整体通向。从P开始的路径比原来少了一个黑色节点，不平衡状态从节点N转移到节点P。可以将P过程修改为case 1，直到遇到根节点，这样递归❿ ❿❿❿ ❿ ❿ P red S black P 是红色， S 为黑色，S 没有非空子节点。这时，只要将P和S的颜色交换一下，空缺就被黑色较少的节点填补，也就是恢复平衡状态：情况5 - P all S 黑色 SL 红色