机器学习算法笔记：树回归

terry 2年前 (2023-09-27) 阅读数 66 #数据结构与算法

在线性回归模型中，假设全局数据是线性的，通过拟合所有样本点得到最终的模型。但实际上，许多问题都是非线性的。在解决这类复杂数据的回归问题时，元素之间的关系并不是简单的线性关系。目前，无法使用全局线性回归模型来拟合此类数据。。

CART树回归算法是一种局部回归算法。通过将全局数据集拆分为多个可以轻松建模的数据集，对每个局部数据集进行局部回归建模。

复杂回归任务

线性回归模型

在基本线性回归算法中，样本特征与样本标签之间存在线性相关性。然而，样本特征和样本标签之间存在非线性关系。关系如图：

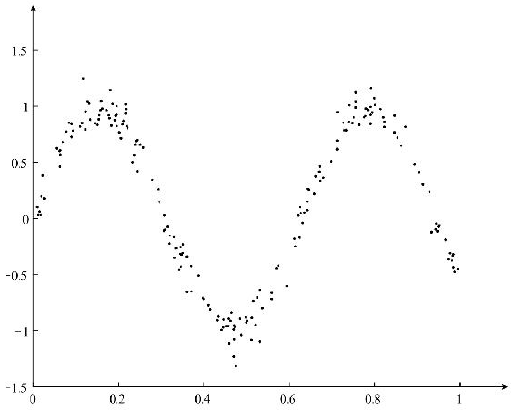
对于上图所示的非线性回归问题，使用简单线性回归的结果如图：

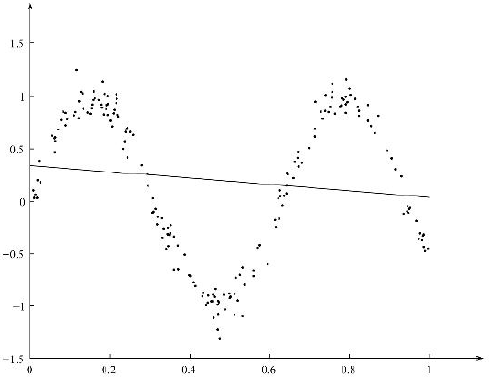
局部加权线性回归

为了能够要实现K拟合非线性数据，可以使用局部加权线性回归。局部加权线性回归的求解结果如图所示：

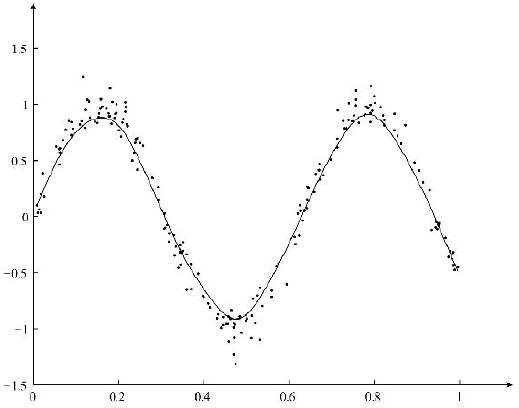
局部加权线性回归可以对非线性数据实现更好的拟合，与简单线性回归不同，与其他算法相比，局部加权线性回归算法是一种局部加权线性回归算法。线性模型，而简单线性回归模型是全局模型。本地模型可能更适合本地数据。虽然局部加权线性回归模型可以更好地拟合非线性数据，但局部加权线性回归模型是一种非参数学习算法。每次预测数据时，都需要使用数据重新训练模型参数。当数据量很大的时候，这样的计算很多时候是非常耗时的。

CART算法

树回归算法也是局部回归算法的一种。它将数据集分为多个部分，并对数据的每个部分分别进行建模。与局部加权线性回归不同，基于树的回归算法是一种基于参数的学习算法。使用训练数据训练模型后，参数一旦确定就无需更改。

分类回归树（CART）算法是常用的树模型。 CART算法既可以处理分类问题，也可以处理回归问题。在决策树算法一文中，我们介绍了如何使用CART算法来解决分类问题。在这篇文章中，我们将重点讨论如何使用CART算法来解决回归问题。 CART算法中的树采用二元递归分割技术，即将当前样本集分为左子树和右子树两组子样本，使得每个生成的非叶子节点都有两个分支。因此，CART算法生成的决策树是一种非典型的二叉树。使用CART算法解决回归问题的主要步骤：①生成CART回归树； ②剪枝CART回归树。

CART回归树生成

CART回归树分裂

CART分类树算法中以基尼指数作为分裂树的索引，根据样本特征对样本进行分裂，直至所有叶子节点所有样本都属于同一类别。然而，在CART回归树中，样本标签是一组连续值，基尼指数不能再作为树分裂的指标。然而，我们注意到基尼指数代表了数据混乱程度的衡量标准。对于连续数据，当数据分布比较分散时，单个数据与均值之差的平方和较大，方差也较大；当数据分布相对集中时，个体数据与均值之差的平方和较小。方差越大，数据波动越大；方差越小，数据波动越小。因此，对于连续数据，样本与均值之差的平方和可以作为划分回归树的指标：

其中 $机器学习算法笔记：树回归$ 是第i个样本的标签， $机器学习算法笔记：树回归$ 是样本 m 标签的平均值。公式用 Python 表示为：

123456789

import numpy as npdef err_cnt(dataSet): '''回归树分区索引 '' 输入：dataSet(list): 训练数据 '' 输出：m*s^2(float ) : 总方差 '' ' data = np.mat(dataSet) return np.var(data[:, -1]) * np.shape(data)[0]

rr_cnt 函数用于计算总方差当前节点。有了分割标准，样本应该如何分割呢？与CART分类树中的方法一样，我们尝试根据每个维度元素中的每个值将样本拆分为树节点的左右子树。比如我们取第j维样本元素中x的均值作为分裂，如果第j维样本值大于等于x，则分裂到右子树，否则分裂进入左子树。分割处理程序如下：

123456789101112131415

def split_tree(data, fea, value): "''根据输入 fea 中的值将数据集 data 分割为左右子树: data(list): 训练示例 "fea (float) : 要拆分的属性索引 Value (float): 指定的拆分值输出: (set_1, set_2)(tuple): 左右子树的聚合 ''' set_1 = [] # 设置右子树 set_2 = [] #为Site Characteristics设置左子树，根据值的大小将样本分为左子树和右子树。当fea上的样本值大于等于该值时，分裂到右子树，否则分裂到左子树。

CART 回归树构建

CART 分类树构建过程如下：

对于当前训练数据集，遍历所有属性和所有可能的分裂点，找到最佳属性分裂及其最佳分裂重点是最小化分割后的基尼指数。利用这个最佳属性及其最佳分割点将训练数据集分割成两个子集，分别对应左子树和左子树。右子树。
对第一步生成的数据的两个子集递归调用第一步，直到满足停止条件。
生成 CART 决策树

为了构建 CART 回归树算法，您必须首先为 CART 回归树中的节点设置结构。其具体实现：

123456789

class node: "''Tree node class ''' def __init__(self, fea=-1, value=None, results=None, right=None, left=None) : self.fea = fea # 用于分割数据集的属性的列索引值 self.value = value #设置分割值 self.results = results #存储叶子节点值 self.right = right #右子树 self.left = left #Left subtree

V为CART回归树的节点类，fea属性代表待分割数据集的属性索引，属性值代表具体的分割值，results属性代表叶子节点的具体值，right属性代表右子树，left属性代表左子树。现在我们来一起实现CART回归树：

1234567891011121314151617181920212223242526272829303132333435363738394041424344

def build_tree(data, min_sample, min_err): '''构建树输入： data(list): 训练样本 min_sample(int): 节点最小样本数 min_err (float ): 最小误差输出: node: 树的根节点 ''' # 构建决策树，函数返回决策树的根节点 if len(data) 0 且 len(set_2) > 0: build_tree(bestSets [0], min_sample, min_err) left = build_tree (BestSets [1], min_sample, min_err) 返回节点 (Fea = Bestcriteria [0], Value = Bestcriteria[1], \ RIGHT = RI ght, left = left) Else: Return node(results=leaf(data)) # 返回当前类别标签作为最终类别标签

build_tree 函数用于构建CART 回归树模型。在CART回归树模型构建过程中，如果某个节点中的单个样本数小于等于指定的最小样本数min_sample，则该节点将不再进行分裂，并使用叶子函数计算当前叶节点的值；当节点需要分裂时，构建过程中首先计算当前节点的误差值。尝试根据每个维度元素的值将样本拆分为左子树和右子树。分裂后，生成左子树和右子树。至此，左右子树的误差值就计算出来了。如果此时误差值小于最优误差值，则更新最优逻辑部分。当节点分裂时，继续Left，右子树分裂：

1234567

def leaf(dataSet): "''计算叶子节点的值输入：dataSet(leaf): 训练样本输出：np.mean( data[:, - 1])(float) :均值 ''' data = np.mat(dataSet) return np.mean(data[:, -1])

当前叶子节点的叶子函数为用于计算值的计算方法是使用partition到叶子节点Label所有样本的平均值

CART回归树剪枝

在CART回归树中，当树中的节点不断分裂样本时，最极端的情况出现的情况是：每个叶子节点只包含一个样本，此时叶子节点的值就是样本标签的值，这种情况下，很容易对训练样本进行“过拟合”。这样训练出来的可以很好的拟合训练样本，但是对于新样本的预测效果会很弱，为了避免生成的CART树回归模型过拟合，通常需要对CART回归树进行剪枝。剪枝是为了防止CART回归树生成过多的叶子节点。剪裁主要分为：前剪裁和后剪裁。

预剪枝

预剪枝是指在CART回归树生成过程中控制树的深度，避免生成过多的叶子节点。在build_tree函数中，我们使用参数min_sample和min_err来控制树中的节点是否需要划分更多。通过不断调整这两个参数，可以找到合适的CART树模型。

剪枝

剪枝就是将训练样本分成两部分。一部分用于训练 CART 树模型。这部分数据称为训练数据，另一部分用于训练生成的CART树模型。剪枝，这部分数据称为验证数据。从上述过程可以看出，在后剪枝过程中，验证生成的CART树模型是否超出了验证数据集。如果发生移植，则合并一些叶节点以实现CART树模型的移植目标。修剪树模型。

参考链接：https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/9.RegTrees/regTrees.py

CART回归树有数据预测❀S有了上面的理论准备，我们利用上面实现的函数来构建CART树的回归模型。使用CART回归树算法解决问题的过程主要包括：①使用训练数据训练CART回归树模型； ②使用经过训练的CART回归树模型来预测新数据。

当训练完CART回归树，需要对训练好的CART回归树模型进行评估时，使用cal_error函数对训练好的CART回归树模型进行评估：

1234567891011121314151617

def cal_error(data, tree): '''评估回归模型树的 CART 输入: data(list): tree: 训练好的 CART 回归树模型输出: err/m(float): 均方根误差 ''' m = len(data) # 样本数 n = len (data [ 0]) - 1 # 样本中的元素数量 err = 0.0 for i in xrange(m): tmp = [] for j in xrange(n): tmp.append(data[i][j]) pre = Predict(tmp, tree) # 计算预测样本值 # 计算残差 err += (data[i][-1] - pre) * (data[i][-1] - pre) return err / m

cal_error 函数用于评估 CART 回归树的训练模型。函数的输入是训练数据和CART回归树模型的训练树。在CART回归树模型评估过程中，使用经过训练的CART回归树模型对每个样本进行预测。预测函数的具体实现如下。当预测完成后，使用预测值和原始样本的标签计算残差。

1234567891011121314151617181920

defpredict(sample,tree):“''预测每个样本样本输入:sample(list):样本树:训练好的CART回归树模型输出:结果(float):预测值'''#1.只是树的根 if tree.results != None: return tree.results else: # 2. 有左子树和右子树 val_sample = sample[tree.fea] # 分支中的值 fea = None # 2.1 选择右子树 if val_sample >= tree.value : Branch = tree.right # 2.2.选择左子分支branch =branch=tree.配对样本进行预测。在预测过程中，主要分为以下几种情况：

如果此时只有根节点存在，则直接返回其值作为最终的预测结果
如果该节点在此时将样本sample中fea索引处的val_sample值与CART回归树模型中分区的值进行比较
- 如果val_sample值大于等于CART回归树模型中的值，选择右子树
- 如果 val_sample 值小于 CART 回归树模型中的值，则选择左子树

最终拟合数据的效果如图：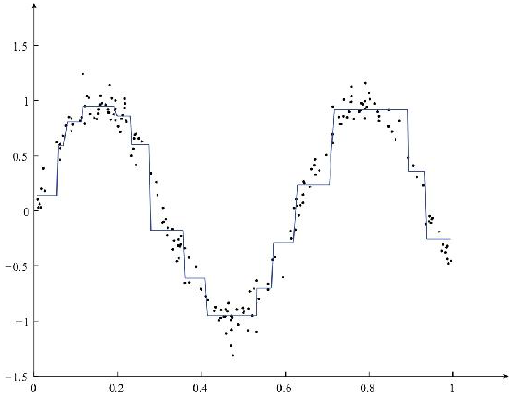

调整min_sample和min_err的值如图：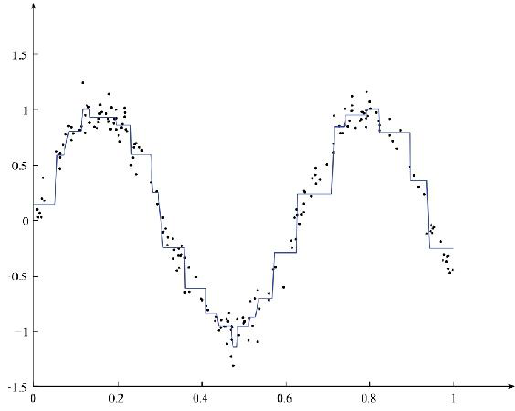

在Python中使用Scikit-Learn实现决策树

分类决策树

1234567891011121314

from sklearn import treefrom sklearn.datasets importlfvizviz_irisimport graph=import load_irisimport graph =irisimport DecisionTreeClassifier(criterion="gini",splitter="best")clf.fit (Iris.data, Iris.Target) DOT_DATA = tree.export_graphviz (CLF, OUT_FILE = NONE, Feature_names = Iris.Feature_names, Class_names = Iris.Target_nam_nam ES , Filled = True, Rounded = TRUE, SPECIAL_CHARACTERS = TRUE) Graph = Graphviz.source (dot_data)graph.view('iris','data')

决策树回归

12345678910111213141516171819202122232425262728

# -*- 编码:utf- 8 -*-from sklearn.datasets import load_bostonfrom sklearn.model_selection 即时通讯端口 train_test_splitfrom sklearn.preprocessing 导入 StandardScalerfrom sklearn.tree 导入 DecisionTreeRegressorfrom sklearn.metrics 导入 r2_score、mean_absolute_error、mean_squared_errorboston = load_boston()X_train、X_test、y_train、y_test2、test_boston。 random_state=33 )ss_X = StandardScaler()ss_y = StandardScaler()X_train = ss_X.fit_transform(X_train)X_test = ss_X.transform(X_test)# fit_transform和transform都需要2D数据操作，目前y_train和y_test都是1D，所以你有调用 reshape(-1,1)，例如： [1,2,3] 变为 [[1],[2],[3]]y_train = ss_y.fit_transform(y_train.reshape(-1, 1)) y_test = ss_y.transform(y_test.reshape(-1, 1))dtr = DecisionTreeRegressor()dtr.fit(X_train, y_train)dtr_y_predict = dtr.predict(X_test)#使用R-squared、MSE、MAE指标评估 print( 'R-squared:', dtr.score(X_test, y_test))print('MSE:',mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(dtr_y_predict)))print('MAE:',mean_absolute_error(ss_y) .inverse_transform(y_test), ss_y.inverse_transform(dtr_y_predict)))

参考：《Python机器学习算法-赵志勇》