机器学习算法学习笔记：逻辑回归

terry 2年前 (2023-09-27) 阅读数 66 #数据结构与算法

虽然逻辑回归算法的名字中含有“回归”二字，但逻辑回归算法实际上是用来解决分类问题的。简单来说，逻辑回归是一种机器学习方法，用于解决二元分类问题（0或1），并用于估计某事物的概率。例如，某个用户购买某种产品的可能性、某个患者感染某种疾病的可能性、用户点击某个广告的可能性等。请注意，这里使用的词是“可能性”，而不是数学上的“概率”。逻辑回归结果并不是数学定义中的概率值，不能直接作为概率值（逻辑回归是基于分布假设的。假设在实际情况下并不那么容易满足，所以在很多情况下，我们得到的逻辑回归输出值不能被认为是真实的概率，只能用作置信水平）。结果通常用作与其他特征值的加权和，而不是直接相乘。

逻辑回归和线性回归是广义线性模型。逻辑回归假设因变量 y 服从伯努利分布，而线性回归假设因变量 y 服从高斯分布。因此，它与线性回归有很多相似之处。如果我们去掉sigmoid映射函数，逻辑回归算法就是线性回归。可以说逻辑回归在理论上得到了线性回归的支持，但逻辑回归通过sigmoid函数引入了非线性因素，因此可以轻松处理0/1分类问题。

逻辑回归的优缺点

优点：

速度快，适合二分类问题
简单易懂，直接看到每个特征的权重
可以轻松将模型更新为吸收新数据

缺点：

对数据和场景的适应性有限制，不如决策算法灵活首先需要介绍一下。我们来看看sigmoid函数，也叫逻辑函数：

它的函数曲线如下：

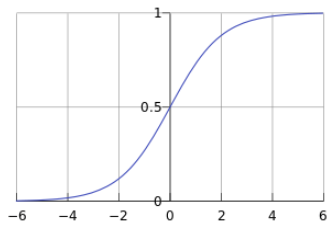
在上图中，可以看到sigmoid函数是一条S形曲线，而它的值在[0, 1]之间，函数的值会很快接近0或远离0的1。它的这个性质对于解决二元分类问题非常重要。

逻辑回归函数的假设形式如下：

所以：

，其中 x 是我们的输入， $机器学习算法学习笔记：逻辑回归$ 是我们需要的参数。机器学习模型实际上将决策函数限制在一组特定的条件下。这组约束条件定义了模型的假设空间。当然，我们也希望这套限制简单合理。逻辑回归模型的假设为：

这个函数的含义是在给定x和 $机器学习算法学习笔记：逻辑回归$ 的条件下，y=1的概率。这里，g(h)就是上面提到的sigmoid函数，对应的决策函数是：

通常的做法是选择0.5作为阈值。在实际应用中，可以根据具体情况选择不同的阈值。如果区分阳性病例的准确率较高，可以选择较高的阈值；如果对阳性案例的召回率要求较高，可以选择较低的阈值。

决策边界

决策边界，也称为决策面，是用于分隔N维空间中不同类别样本的平面或曲面。注意：决策边界是假设函数的属性，由参数决定，而不是数据集的特征。这里我们引用吴恩达课程中的两个图来解释这个问题：

线性决策边界

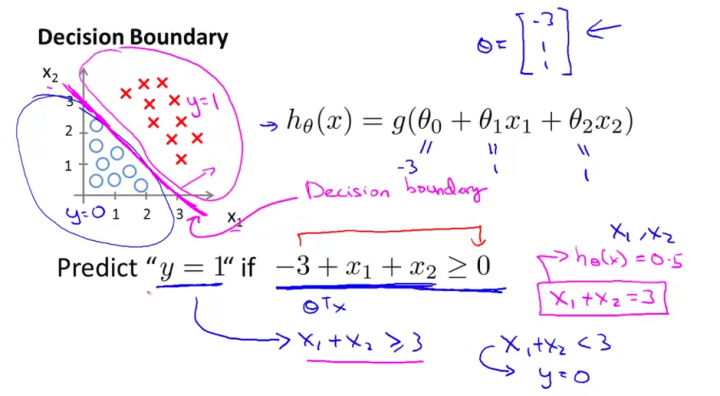
这是决策边界： $机器学习算法学习笔记：逻辑回归$

非线性决策边界

这是决策边界： $机器学习算法学习笔记：逻辑回归$

上面两个数字清楚地说明了决策极限是什么。决策边界实际上是一个方程。在逻辑回归中，决策边界由 $机器学习算法学习笔记：逻辑回归$ 定义：

这里要注意理解假设函数以及决策边界函数的区别和联系。决策边界是假设函数的一个属性，由假设函数的参数 ( $机器学习算法学习笔记：逻辑回归$ ) 确定。

在逻辑回归中，假设函数 $机器学习算法学习笔记：逻辑回归$ 用于计算样本属于某个类别的概率；决策函数 $机器学习算法学习笔记：逻辑回归$ 用于计算（给定的）样本类别；决策边界 $机器学习算法学习笔记：逻辑回归$ 是方程它用于识别分类函数（模型）的分类边界。

损失函数（Cost function）

Logistic回归假设为： $机器学习算法学习笔记：逻辑回归$ 。我们的任务是找到一个“合适的” $机器学习算法学习笔记：逻辑回归$ ，让这个假设尽可能地解决我们的问题。例如，在分类任务中，我们希望一个决策边界能够最大限度地分离数据。那么如何用数学方式表达这个要求呢？在线性回归中，通常使用均方误差来估计 $机器学习算法学习笔记：逻辑回归$ 的质量：

这意味着 $机器学习算法学习笔记：逻辑回归$ 越小， $机器学习算法学习笔记：逻辑回归$ 越好。那为什么不直接用均方误差代替 $机器学习算法学习笔记：逻辑回归$ 逻辑回归呢？原因是这样生成的 $机器学习算法学习笔记：逻辑回归$ 是非凸函数。举个例子：

12345678910111213

patterns = [(-5, 1), (-20, 0), (-2, 1)]def sigmoid(theta, x): return 1/(1 + math.e* *( - theta*x))def cost(theta): diffs = [(sigmoid(theta, x) - y) for x,y in Samples] return sum(diff * diff for diff in diffs)/len(samples) /2X = np.arange(-1, 1, 0.01)Y = np.array([X 中的 theta 的 cost(theta)])plt.plot(X, Y)plt.show()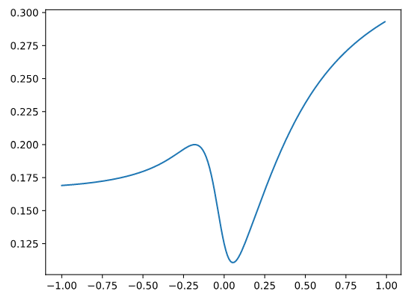

可以是可见这个损失函数不是凸的，局部极小值和全局极小值不一样，所以很难用梯度下降法来求解。因此，逻辑回归模型使用以下损失函数，

，写成统一形式：

那么损失函数如何影响决策呢？首先，损失函数是对 hθ(x) 做出错误推断的惩罚。因此，损失越小，一般来说 hθ(x) 的确定就越正确。上面的公式意味着损失越小，最终的表面 hθ(x) 就越接近数据点，换句话说，它就会“更陡”：

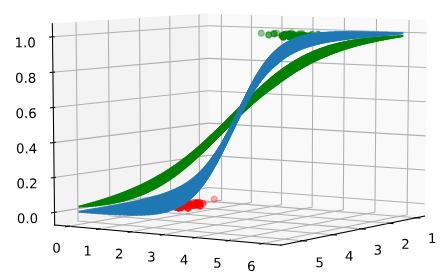
在这张图像中，有 $机器学习算法学习笔记：逻辑回归$ ，它是蓝色的。该区域对应的损失 $机器学习算法学习笔记：逻辑回归$ 小于绿色区域对应的值 $机器学习算法学习笔记：逻辑回归$ 。正如您所看到的，损失较小的蓝色表面更陡峭。

损失函数对决策边界有什么影响？我们取决策边界 $机器学习算法学习笔记：逻辑回归$ ，我们看到决策边界也略有不同：

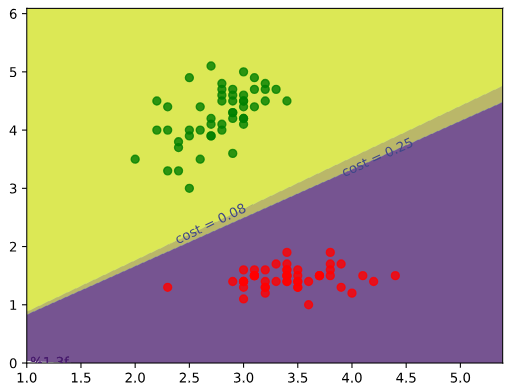
，但是由于这两个 $机器学习算法学习笔记：逻辑回归$ 可以区分两组数据，所以它们之间没有特别大的差异。我假设在训练逻辑回归时，前几次迭代应该能够快速形成决策边界。接下来几次重复的作用应该是让 $机器学习算法学习笔记：逻辑回归$ “更陡”。盲目追随较小的损失是否有助于决策边界？？

总结一下，如何确定模型的损失函数？首先，损失函数必须正确评估参数，使得损失较小的参数对解决问题更有用；另一方面，受优化方法的限制，损失函数需要可解。当然，一些常用的模型损失函数也已经被粗略地定义了。

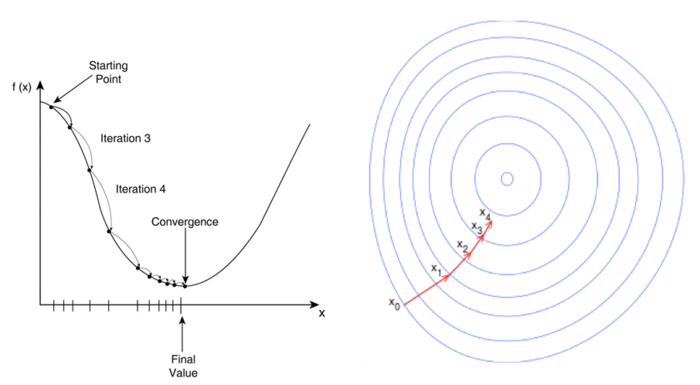
梯度下降

与线性回归类似，我们使用梯度下降算法来求解逻辑回归模型的参数。有关梯度下降的更多信息，请参阅线性回归文章。

正则化（Regularization）

如果模型参数太多，我们很容易遇到过拟合问题。目前需要一种方法来控制模型的复杂度。典型的方法是将正则表达式添加到优化目标中，并通过惩罚过大的参数来避免过度拟合。

一般情况下，p=1或p=2分别对应L1和L2的排列。从下图可以看出两者的区别。 L1调节（左图）倾向于使参数变为0，从而可以产生稀疏解。

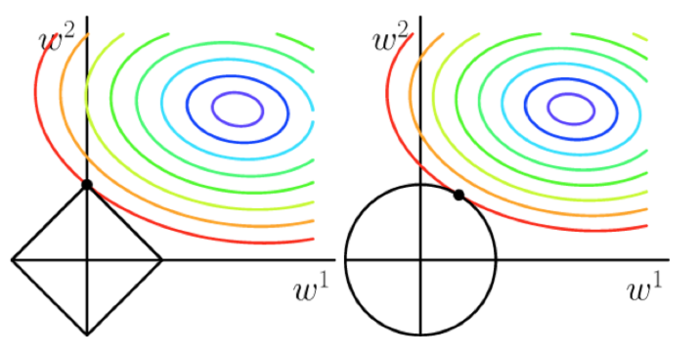
有关正则化的详细信息，请参阅岭回归和套索回归文章。

使用 Scikit-Learn 的逻辑回归

在 scikit-learn 中，逻辑回归模型是通过 sklearn.linear_model.LogisticRegression 类实现的。

正则项权重

正则项权重 $机器学习算法学习笔记：逻辑回归$ ，这对应逻辑回归中的参数C，但成反比。这意味着C的值越大，正则表达式的权重越低，模型容易出现过拟合； C的值越小，正则表达式的权重越大，模型容易欠拟合。

L1/L2范数

构建逻辑回归模型时，对于值为“l1”或“l2”的参数存在惩罚。这实际上定义了我们之前介绍的正则表达式的形式。

最简单的使用方法：

123456789101112131415

from sklearn.datasets import make_classificationfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LogisticRegressionnb_samples = 500X, Y = make_classification(n_samples=nb_samples, n_features=2, n_informative= 2、n_redundant=0， n_clusters_per_class=1)X_train, 样本的准确率 test_score = lr.score(X_test, Y_test) # 模型在测试集上的准确率 print(train_score)print(test_score)

可以选择 LogisticRegressionCV 或 GridSearchCV

GridSearchCV :

12345678910111213141516

from sklearn.datasets import load_irisfrom sklearn.linear_model import LogisticRegressionfrom sklearn.model_selection import GridSearchCVimport numpy as npiris = load_iris()param_grid = { 'penalty': ["l" 1", "l2"], 'C': np.power(10.0, np.arange(-10, 10))}gs = GridSearchCV(估计器=LogisticRegression(), param_grid=param_grid, 评分='准确度', cv=10)gs.fit(iris.data, iris.target)print(gs.best_estimator_)

LogisticRegressionCV:

12345678910111213141516171819202122

from sklearn.datasets import load_irisfrom sklearn.linear_model import LogisticRegressionCVfrom sklearn. model_selection 导入 KFoldimport numpy as npiris = load_iris()fold = KFold(n_splits=5, shuffle=True, random_state=777)searchCV = LogisticRegressionCV( Cs=list(np.power(10.0, np.arange(-10, 10)) ），惩罚='l2'，评分='roc_auc'，cv=fold，random_state=777，max_iter=10000，fit_intercept=True，solver='newton-cg'，tol=10）searchCV.fit（iris.data， iris.target)print('Max auc_roc:', searchCV.scores_[1].mean(axis=0).max())

参考链接：