二叉搜索树算法讲解及Go代码示例

terry 2年前 (2023-09-27) 阅读数 62 #数据结构与算法

Kaylyn以Go代码为例，直接讲解二叉搜索树算法。

简介

在过去的一年里，Kaylyn一直试图通过实施各种算法来击败找乐子。这对你来说可能听起来很奇怪，但算法对她来说尤其陌生。她特别讨厌大学课堂上的算法。她的教授经常使用复杂的术语来教学，并且拒绝解释一些“显而易见”的概念。因此，她只学到了有助于她找到工作的基础知识。

然而，当她开始使用 Go 来实现这些算法时，她的态度开始改变。将用 C 或 Java 编写的算法转换为 Go 出奇地容易，因此她逐渐开始比在大学时更彻底地理解这些算法。

Kaylyn解释了为什么会发生这种情况，并向您展示如何使用二叉搜索树。在此之前，我们要问：为什么算法的学习体验这么差？

学习算法很可怕

此屏幕截图来自《算法导论》的二叉搜索树部分。《算法导论》被认为是算法书籍中的圣经。作者表示，在1989年出版之前，还没有一本好的算法教科书。但读过《算法导论》的人都知道，它是教授写的，他的主要读者是学术界人士。

一些示例：

本页引用了本书其他地方定义的许多术语。所以你需要了解：
- 什么是卫星数据
- 什么是链表
- 什么是前序和后序树遍历
如果你不在每一页都做笔记书，你无法知道它是什么。
如果您像Kaylyn一样，那么当您阅读此页面时，您要做的第一件事就是查看代码。然而，页面上的单个代码仅解释了一种遍历二叉搜索树的方法，而不是二叉搜索树的实际含义。
本页的整个下四分之一都是定理和证明，这可能是出于好意。许多教科书的王者认为向你证明他们的陈述是正确的非常重要；否则你不能相信他们。算法应该是一本入门教科书，这是可笑的。但初学者不需要了解有关正确使用算法的所有细节，因为他们会听你的。
他们有一个两句话区域（以绿色框突出显示），解释了二叉搜索树算法是什么。但它隐藏在一个几乎看不见的句子中，被称为二叉搜索树的“属性”，这对于初学者来说是一个非常令人困惑的术语。

结论：

学术教材王牌不一定是好老师，最好的老师往往不写教材。
遗憾的是，大多数人都抄袭标准教科书中使用的教学风格或格式。在查看二叉搜索树之前，他们假设您已经了解相关术语。事实上，这些“必需的知识”大部分都是不必要的。

本讲座的其余部分将讨论二叉搜索树。如果您是 Go 新手或算法新手，这将对您有用。如果您两者都不是，那么这可以作为一个很好的评论，同时与其他对 Go 或算法感兴趣的人分享。

猜测

这是演讲结束前你唯一需要知道的事情。

这是一个“猜谜游戏”，很多人小时候都玩过的游戏。您邀请您的朋友参加一个游戏，猜测一个范围内的特定数字（例如从 1 到 100）。然后你的朋友可以说“57”。通常第一次猜测是错误的，但是你告诉他们他们猜测的数字是否太高或太低。然后他就可以继续猜测，直到他最终猜对为止。

这个猜谜游戏基本上是一个二分查找的过程。如果你正确理解了这个难题，你也将能够理解二叉搜索树算法的原理。你的朋友猜到的数字是搜索树中的一个节点。 “更高”和“更低”决定移动方向：右节点或左节点。

二分搜索树规则

每个节点都包含一个唯一的键，用于比较不同的节点大小。键可以是任何类型：字符串、整数等。
每个节点最多有两个子节点
该节点的值小于右子树的节点的值
该节点node的值大于右子树的节点的值左子树
没有重复键

二分查找树包含三个主要操作：

查找
删除删除插入可以更快地完成上述三个操作，这就是为什么它们这么受欢迎。上面的
查找
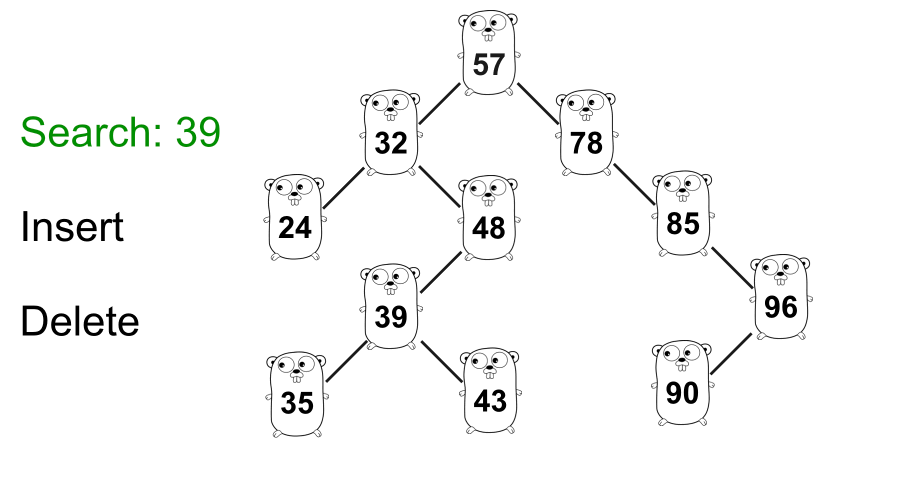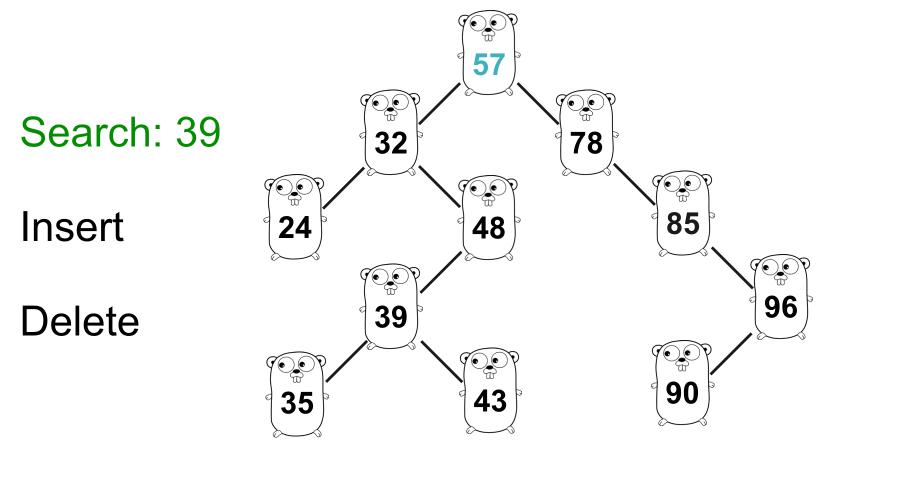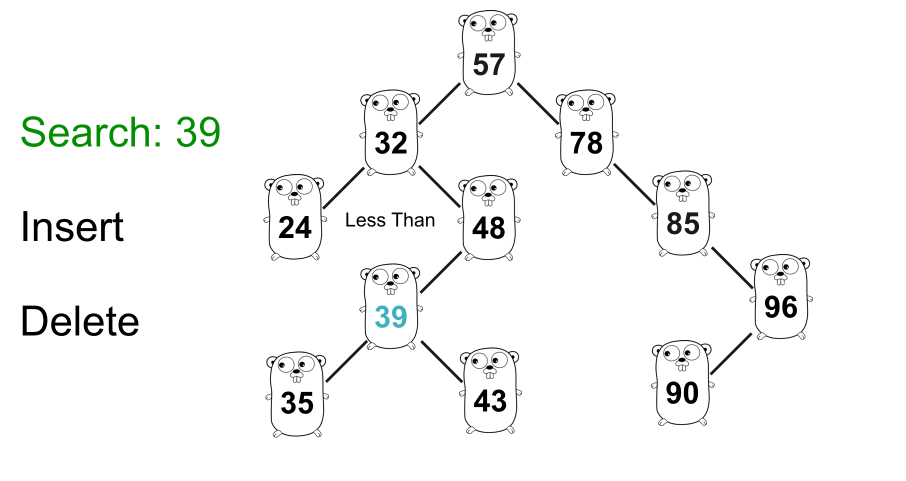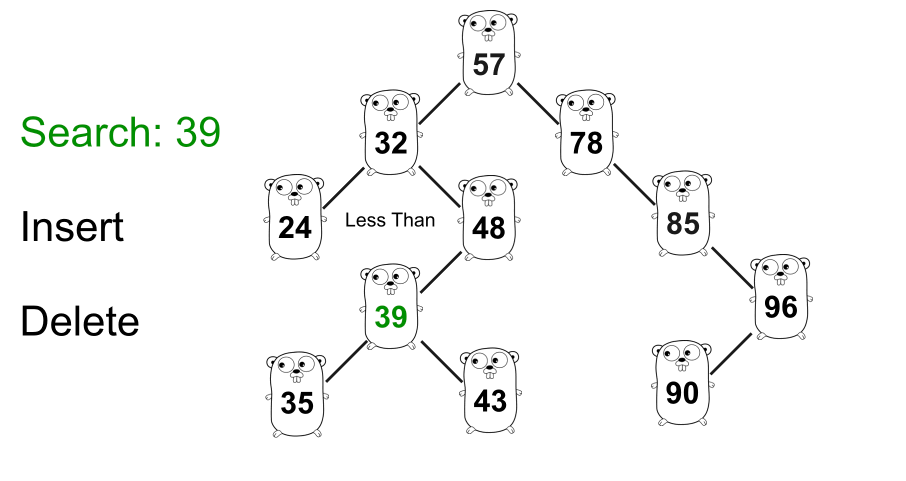
GIF 显示了在树种中搜索 39 的示例。
二叉搜索树的一个非常重要的性质是，某个节点的右子树中的节点的值总是大于该节点本身的值，而左子树中的某个节点的值总是小于比节点本身的值。例如图中，右边的数字57总是大于57，而左边的数字总是小于57。
此属性对于树中除根节点之外的每个节点都有效。上图中，所有右子树的值都大于32，左子树的值都小于32。
好了，我们知道了基本原理，可以开始写代码了。
```
type Node struct {
    Key   int
    Left  *Node
    Right *Node
}
复制代码
```
的基本结构是 stuck ，如果你还没有使用过stuck，原则上可以解释为这个结构你所需要的就是键（比较其他节点）、左和右。
定义节点时，可以使用如下文字表达式：
```
tree := &Node{Key: 6}
复制代码
```
为 6 from from 创建 Key 您可能想知道和去了。交通。事实上，它们都被初始化为零值。
```
tree := &Node{
    Key:   6,
    Left:  nil,
    Right: nil,
}
复制代码
```
但是，您也可以显式指定这些字段的值（例如上面指定了Key）。
或者输入不带字段名称的字段值：
```
tree := &Node{6, nil, nil}
复制代码
```
在这种情况下，第一个参数是 Key，第二个参数是第三个❙❀，❀ 第三个是正确。
输入后，您可以通过点语法访问它们的值：
```
tree := &Node{6, nil, nil}
fmt.Println(tree.Key)
复制代码
```
现在让我们实现搜索算法搜索示例G❙显示了将81插入上面的图像G❙一个号码。插入与搜索非常相似。我们想要找到 81 应该插入的位置，因此我们开始搜索并将其插入到适当的位置。
```
func (n *Node) Insert(key int) {
    if n.Key < key {
        if n.Right == nil { // 我们找到了一个空位，结束！
            n.Right = &Node{Key: key}
            return
        }
        // 向右边找
        n.Right.Insert(key)
       	return
    } 
    if n.Key > key {
        if n.Left == nil { // 我们找到了一个空位，结束
            n.Left = &Node{Key: key}
            return
        } 
        // 向左边找
        n.Left.Insert(key)
    }
    // 如果 n.Key == key，则什么也不做
}
复制代码
```
如果您还没有看过语法 (n *Node)，您可以在此处查看指针接收器说明。
删除
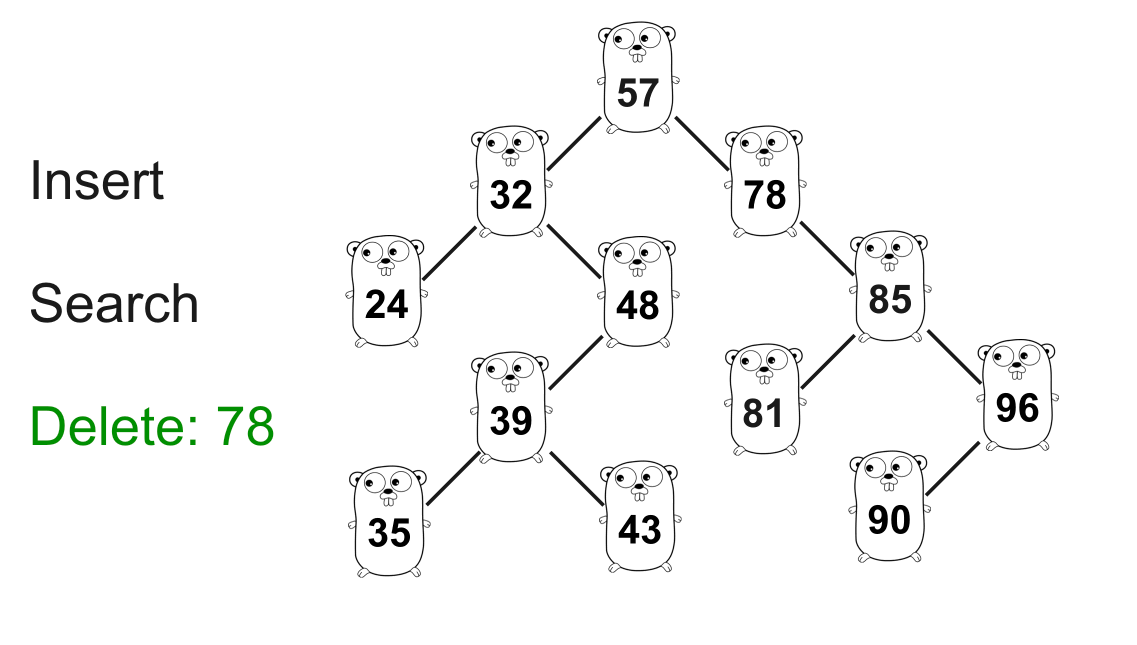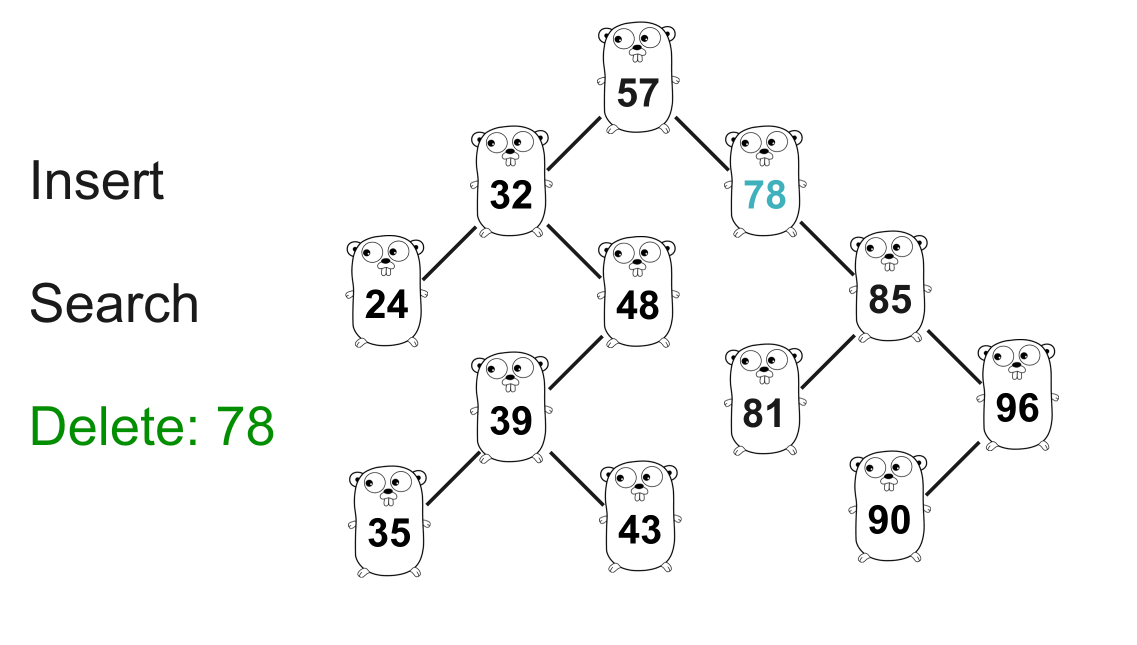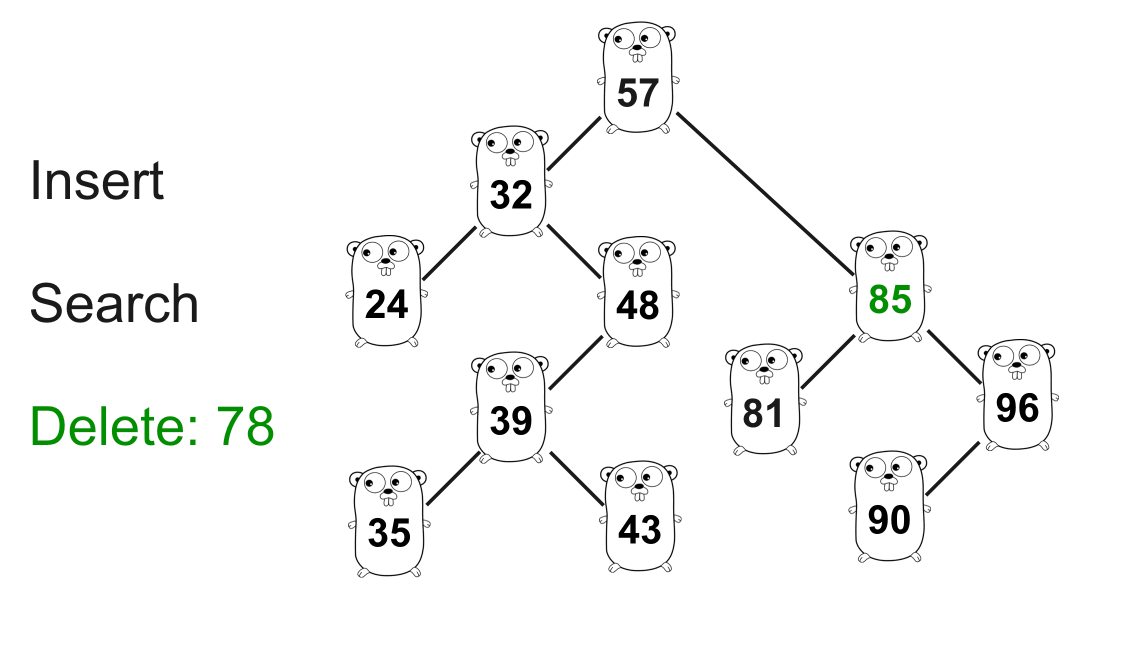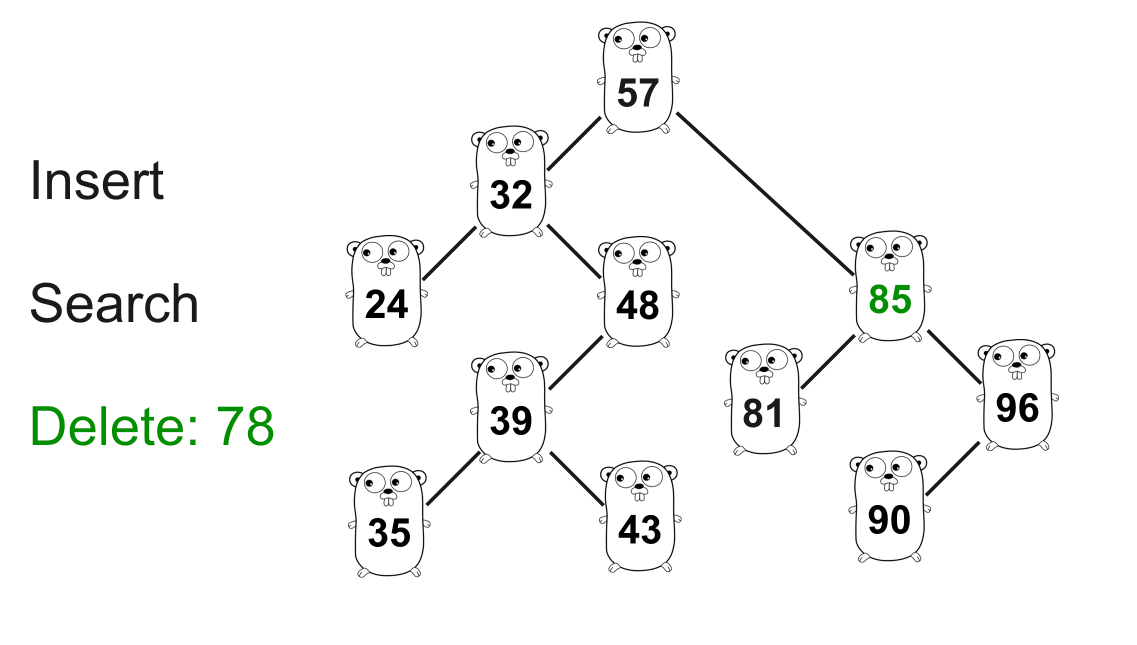
上面的 GIF 显示了从树中删除 78。 78 的搜索过程与之前类似。在这种情况下，我们只需要把78从树上正确地“切掉”，并将正确的子节点57连接到85即可。 func (n *Node) Delete(key int) *Node { // 按 `key` 查找 if n.Key < key { n.Right = n.Right.Delete(key) return n } if n.Key > key { n.Left = n.Left.Delete(key) return n } // n.Key == `key` if n.Left == nil { // 只指向反向的节点 return n.Right } if n.Right == nil { // 只指向反向的节点 return n.Left } // 如果 `n` 有两个子节点，则需要确定下一个放在位置 n 的最大值 // 使得二叉查找树保持正确的性质 min := n.Right.Min() // 我们只使用最小节点来更新 `n` 的 key // 因此 n 的直接子节点不再为空 n.Key = min n.Right = n.Right.Delete(min) return n } 复制代码最小值向左移动，会找到最小值（图中24） func (n *Node) Min() int { if n.Left == nil { return n.Key } return n.Left.Min() } 复制代码最大值 func (n *Node) Max() int { if n.Right == nil { return n.Key } return n.Right.Max() } 复制代码向右移动，会找到最大值（图中96）。单元测试现在我们已经编写了每个主要二叉搜索树函数的代码，让我们实际测试我们的代码！实践中测试最有趣的部分是：Go 中的测试比 Python 和 C 等许多其他语言更容易。 // 必须导入标准库 import "testing" // 这个称之为测试表。它能够简单的指定测试用例来避免写出重复代码。 // 见 https://github.com/golang/go/wiki/TableDrivenTests var tests = []struct { input int output bool }{ {6, true}, {16, false}, {3, true}, } func TestSearch(t *testing.T) { // 6 // / // 3 tree := &Node{Key: 6, Left: &Node{Key: 3}} for i, test := range tests { if res := tree.Search(test.input); res != test.output { t.Errorf("%d: got %v, expected %v", i, res, test.output) } } } 复制代码然后运行： > go test 复制代码 Go 将运行您的测试并输出标准格式的结果，告诉您测试是否通过、测试失败消息以及测试花费了多长时间。性能测试还有更多！ Go 可以让性能测试变得非常简单，你只需要： import "testing" func BenchmarkSearch(b *testing.B) { tree := &Node{Key: 6} for i := 0; i < b.N; i++ { tree.Search(6) } } 复制代码 b.N 反复运行 tree.Search() 即可获得稳定性操作树。结果。使用以下命令运行测试： > go test -bench= 复制代码输出将如下所示： goos: darwin goarch: amd64 pkg: github.com/kgibilterra/alGOrithms/bst BenchmarkSearch-4 1000000000 2.84 ns/op PASS ok github.com/kgibilterra/alGOrithms/bst 3.141s 复制代码您需要关注的是以下行： BenchmarkSearch-4 1000000000 2.84 ns/op 复制代码它显示了函数执行的速度。在这种情况下，test.Search()的执行时间约为 2.84 纳秒。现在您可以轻松地运行性能测试了，您可以开始做一些实验，例如：如果树非常大或非常深灰色会发生什么？如果我更改需要查找的密钥会怎样？对于理解映射和切片之间的性能特征特别有用。希望您能很快在互联网上找到相关反馈。译者注：二叉搜索树中插入、删除、查找的时间复杂度为O(log(n))，最坏情况为O(n)； Go的map是一个哈希表，我们知道哈希表中插入、删除和查找的平均时间复杂度是O(1)，最坏情况是O(n)；而搜索Go段需要遍历段，插入和删除的复杂度都是O(n)。如果需要，内存会重新分配，最坏情况为 O(n)。二叉搜索树术语最后，让我们看一下二叉搜索树术语。如果你想了解更多关于二叉搜索树的知识，以下术语很有用：树高：从根节点到叶子节点的最长路径的边数，它决定了算法的速度。图中树的高度5。节点深度：从根节点到节点的边数。 48 的深度为 2。完全二叉树：每个非叶子节点包含两个子节点。完全二叉树：每一层的节点都被完全填满。如果最后一层未满，则仅缺少右侧的几个节点。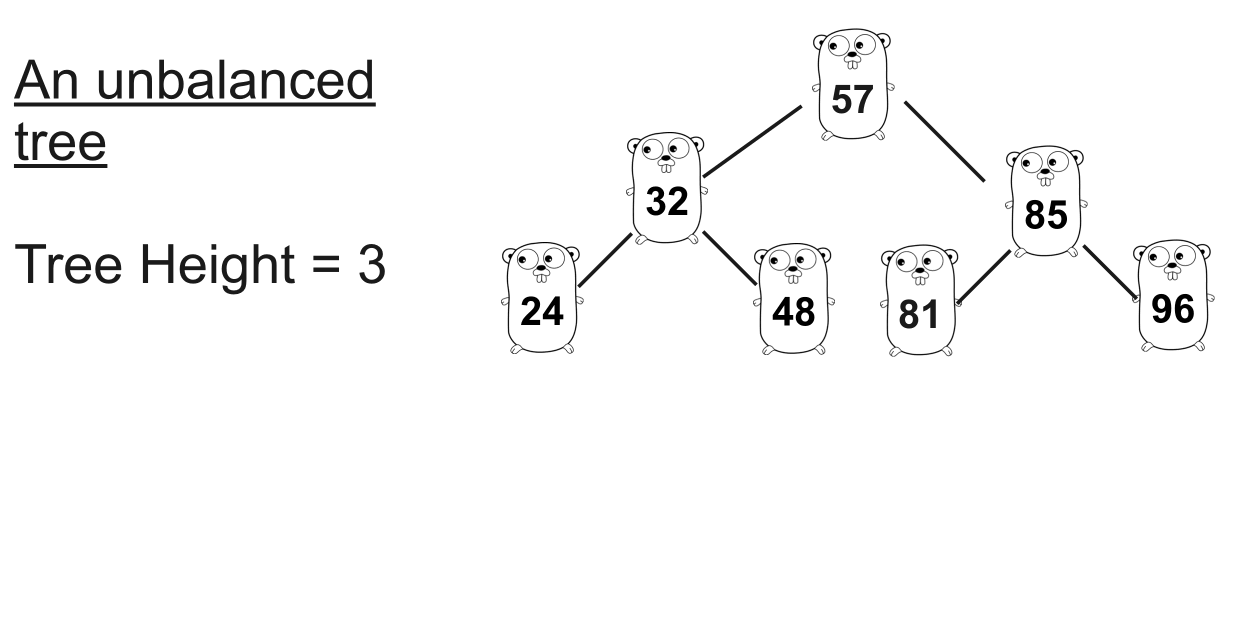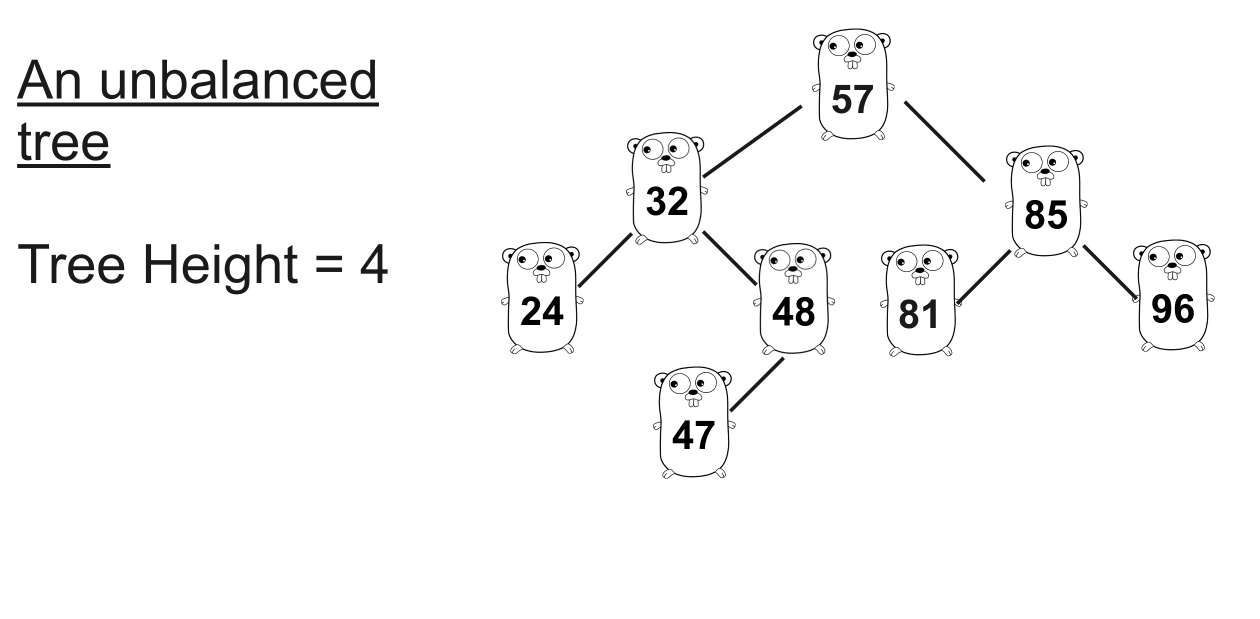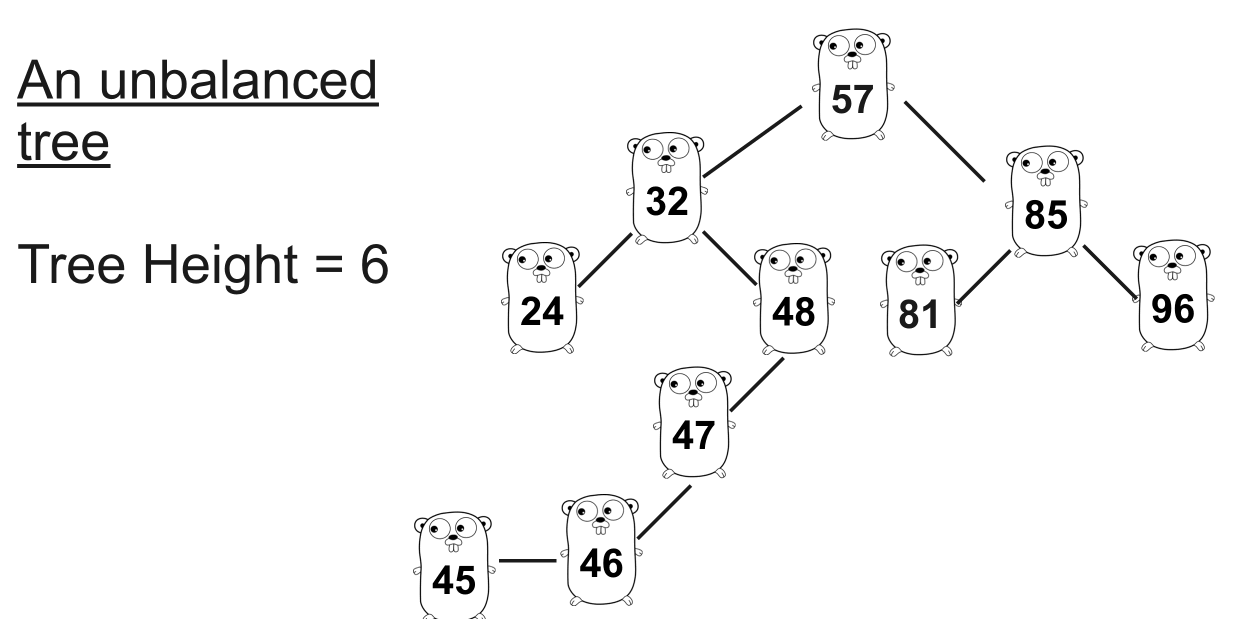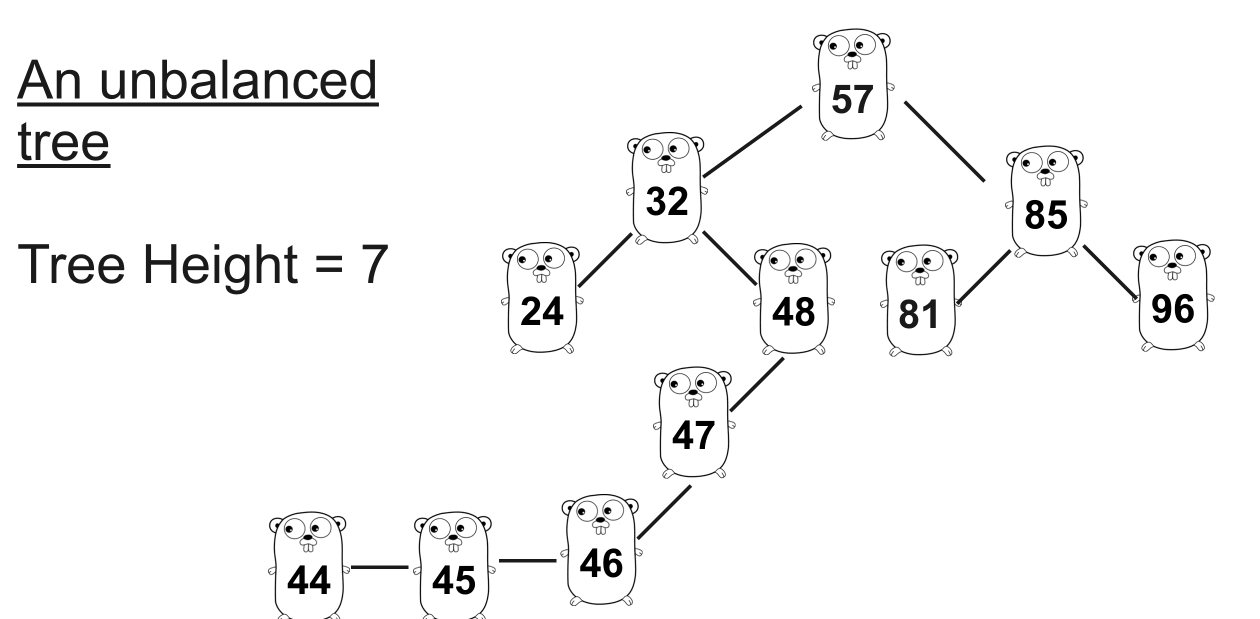不平衡树想象一下您正在这棵树中寻找47。可以看到，找到需要七步，而找到 24 只需要三步。随着它的增加，平衡变得严重。解决方案是使树平衡：平衡树：该树包含与不平衡树相同的节点，但在平衡树上搜索平均比在不平衡树上搜索更快。作者：欧长坤链接：https://juejin.im/post/5b94de9c5188255c5047076c 来源：掘金来源：掘金商业转载请联系作者授权。非商业转载请注明出处。