深度机器学习系列——异常检测(AnomalyDetection)
异常检测(AnomalyDetection)是机器学习的一个重要分支,有着广泛的实际应用,与我们的生活息息相关。那么什么是异常检测呢?目前面临的主要方法和技术问题是什么?这篇文章或许可以提供一些参考。 定义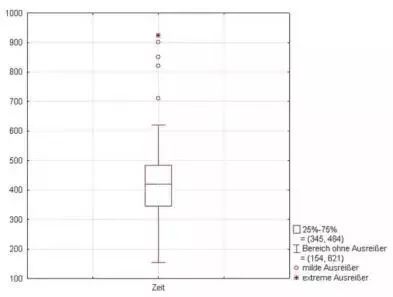 2.统计方法:单变量/多元高斯分布总体思路
2.统计方法:单变量/多元高斯分布总体思路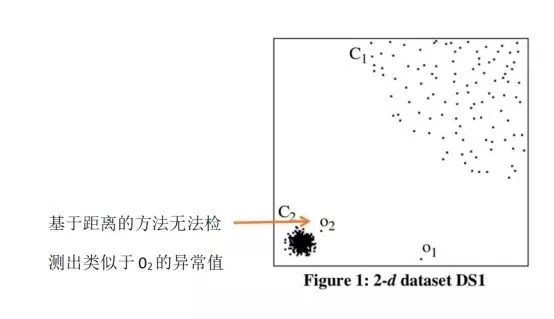 4。基于密度的方法:局部离群因子 (LOF) 总体思路
4。基于密度的方法:局部离群因子 (LOF) 总体思路
- 离群值
霍金斯的定义是:“离群值是指与其他观察结果显着不同的观察结果,从而引起人们怀疑它是由不同机制产生的。”
- 异常检测
所谓异常检测就是找到与大多数对象不同的对象,即找到异常值。通常认为数据具有“正常”模型,偏差被认为是与该正常模型的偏差。实际应用中异常的定义也是具体的。![]() 应用领域
应用领域
- 网络入侵检测
- 保险/信用卡欺诈检测
- 医疗保健信息获取/医疗诊断
- 工业损害检测
- 图像处理/视频监控
- 很难定义具有代表性的“正常”区域
- 正常和异常行为之间的界限通常不明确
- 异常值的确切定义因应用领域而异
- 难以获得训练/验证标签数据
- 数据可能包含噪声
- 正常行为不是静态的,会不断演化和变化
4。基于密度的方法:LOF
5。基于模型的方法:孤立森林,RNN1。图形方法:Boxplot
- Square 盒子的底部和顶部分别是 Q1(下四分位数)和 Q3(上四分位数)
- 盒子内部的线段是第二四分位数(中位数)
- 大于分位数+1.5IQR或小于顶部四分位数-1.5IQR的底部四个值是异常值(四分位数范围IQR=Q3-Q1)
- 熟悉给定的统计分布(如高斯分布)
- 假设所有数据点均由该分布生成(如均值和标准差),进行参数计算
- 异常值是整体的下端分布概率
基本假设
- 正常数据点遵循(已知)分布并出现在模型的高概率区域中
- 异常值偏离此分布
1. 单变量高斯分布
(1 ) 选择能够代表异常实例的特征xj
(2)。用参数 u1, …, un, σ12, …, σn2 进行调整 ![]() (3) 如果知道新实例 x,则计算 p(x)
(3) 如果知道新实例 x,则计算 p(x)![]() (4) 如果 p(x) 2。多元高斯分布
(4) 如果 p(x) 2。多元高斯分布 ![]()
![]() 3。问题
3。问题
- 平均值和标准差与异常值 非常敏感。
- 这些值是针对整个数据集计算的,包括潜在的异常值。
- 选择正确的ε值是很困难的。
- 数据分布未知。?密集邻域
- 离群值距离其相邻点较远,即具有稀疏邻域
实现方法
- 计算每对数据点之间的距离
定义离群值的各种方法
- 点给定距离内少于 p 个相邻点的数据点为 D 个离群值
- 与第 k 个相邻点距离最大的前 n 个点为离群值
- 与 k 个最近邻点的平均距离最大的数据点为离群值
问题
- 此假设并不一定在所有情况下都成立。
- 计算每对数据之间的距离是昂贵的。
- 维数灾难的问题,即随着维数的增加,计算量呈指数级增长。
- 将给定点周围的密度与其局部相邻点周围的密度进行比较
- 该点及其相邻点 相对密度计算为异常得分
基本假设
- 正常数据点的密度与其邻居的密度相似
- 异常点的密度与其邻居的密度有很大不同
1。对于距离p点的第k个点 距离
点p的第k个距离(k为正整数),表示为k-distance(p),定义为点p到点的距离d(p,o) oε D,使得:
(1) 集合中除 p 之外至少有 k 个点 o'εD 满足 d(p,o,)≤d(p,o) 且
(2 ) 集合 k−1 个点 o'∈D 中最多不存在包含 p 满足 d(p,o,)
版权声明
本文仅代表作者观点,不代表Code前端网立场。
本文系作者Code前端网发表,如需转载,请注明页面地址。
 code前端网
code前端网



